Molnár Zsófia alábbi írása – minimális változtatásokkal – a félévközi nagy, számítógépes házi feladat egy igazán szép megoldása. A feladat a SIR modell differenciálegyenlet-rendszerének számítógépes megoldása volt, az előre megadott A) ![]() és a hallgató által megállapított és megindokolt B)
és a hallgató által megállapított és megindokolt B) ![]() kontaktusmátrix mellett, ez utóbbi esetben az egészségügyi ellátórendszer terhelhetőségét is figyelembe véve.
kontaktusmátrix mellett, ez utóbbi esetben az egészségügyi ellátórendszer terhelhetőségét is figyelembe véve.
A Nemlineáris Dinamikai Modellek a Biológiában minden tavaszi félévben szabadon választható tantárgy a Pázmány Péter Katolikus Egyetem Információtechnológia Kar bionikus mérnökképzésének BSc hallgatói részére. Idén a tárgyat 14 hallgató választotta és mindenki ugyanazt kapta házi feladatul. A feladat A) részét csak egyféleképpen lehetett kezelni, de a B) rész – egy járvány kontaktusmátrixának korlátozása, hat szabad paraméterrel – tág teret engedett a diákok fantáziája és számítógépes kísérletező kedve számára. A feladat megfogalmazásában tudatosan kerültem a koronavírus és a Magyarország szavakat. Ezáltal is félreérthetetlenné akartam tenni, hogy semmilyen járvány lefutása sem írható le azzal a játékmodellel (toy model), amelynek vizsgálatát a hallgatóktól kértem. A feladat összes konkrét paraméterértéke az én fejemben született meg. Közben persze csak sandítottam a valóságra, de Molnár Zsófia volt az, aki a ![]() megbetegedési tényező általam eredetileg
megbetegedési tényező általam eredetileg ![]() -nek javasolt értékének módosítását kérte tőlem. A közkeletű fertőzési ráta kifejezést is szándékosan nem használtam, már csak azért sem, mert a
-nek javasolt értékének módosítását kérte tőlem. A közkeletű fertőzési ráta kifejezést is szándékosan nem használtam, már csak azért sem, mert a ![]() paraméter a
paraméter a ![]() kontaktusmátrix elemeivel „összekuszálva jut be” a SIR modell fertőzhető–fertőzött találkozásainak dinamikájába.
kontaktusmátrix elemeivel „összekuszálva jut be” a SIR modell fertőzhető–fertőzött találkozásainak dinamikájába.
A járványterjedés SIR-modellje és a kontaktusmátrix korlátozása
A SIR-modell egyike a legegyszerűbb epidemiológiai modelleknek, és sok más modell alapjául szolgál. A modell három tényezőből épül fel: ![]() a fertőzhetők száma (Suspected),
a fertőzhetők száma (Suspected), ![]() a fertőzöttek száma (Infected) és
a fertőzöttek száma (Infected) és ![]() a gyógyultak száma (Recovered). A modell segítségével meglehetősen jól előre jelezhető egy járvány terjedése. Az
a gyógyultak száma (Recovered). A modell segítségével meglehetősen jól előre jelezhető egy járvány terjedése. Az ![]() változó együttesen tartalmazza a valóban gyógyultakat és az elhunytakat. A gyógyulás tartós gyógyulást, immunitást jelent a betegségre nézve. Bemutatom a SIR-modell három korosztályos, kontaktusmátrixos változatát és azt is, hogy a kontaktusmátrix elemeinek csökkentése valóban ellaposítja a járványt, így még a járvány csúcsa is az egészségügyi ellátó-rendszer terhelhetőségi korlátján belül marad.
változó együttesen tartalmazza a valóban gyógyultakat és az elhunytakat. A gyógyulás tartós gyógyulást, immunitást jelent a betegségre nézve. Bemutatom a SIR-modell három korosztályos, kontaktusmátrixos változatát és azt is, hogy a kontaktusmátrix elemeinek csökkentése valóban ellaposítja a járványt, így még a járvány csúcsa is az egészségügyi ellátó-rendszer terhelhetőségi korlátján belül marad.
A) feladatrész
A folytonos idejű korosztályos, kontaktmátrixos SIR modell alatt az alábbi ![]() differenciálegyenletrendszert értjük (amely tehát
differenciálegyenletrendszert értjük (amely tehát ![]() egyenletből áll):
egyenletből áll):
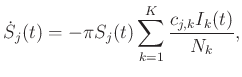
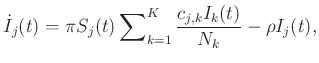
Az alsó indexek a korosztályokat jelzik: a teljes populációt felbontottuk ![]() korosztályra, ahol a
korosztályra, ahol a ![]() indexű jelenti a legfiatalabbat, a
indexű jelenti a legfiatalabbat, a ![]() pedig a legidősebbet. Az
pedig a legidősebbet. Az ![]() jelöli az egyedszámot a
jelöli az egyedszámot a ![]() -adik korosztályban. Feltesszük, hogy a korosztályok között nincsen átmenet (relatíve rövid idő alatt játszódik le), így az egyedszám konstansnak vehető:
-adik korosztályban. Feltesszük, hogy a korosztályok között nincsen átmenet (relatíve rövid idő alatt játszódik le), így az egyedszám konstansnak vehető: ![]() .
.
A megbetegedési rátát ![]() -vel, a gyógyulási rátát
-vel, a gyógyulási rátát ![]() -val jelöljük. Ezek függetlenek az érintett korosztálytól, mindenhol ugyanakkorák.
-val jelöljük. Ezek függetlenek az érintett korosztálytól, mindenhol ugyanakkorák.
A ![]() mátrixot nevezzük kontaktusmátrixnak, ennek
mátrixot nevezzük kontaktusmátrixnak, ennek ![]() -adik sorának
-adik sorának ![]() -edik eleme azt jelenti, hogy a
-edik eleme azt jelenti, hogy a ![]() -adik korosztályba tartozó egyednek egy nap alatt átlagosan hány kontaktusa van a
-adik korosztályba tartozó egyednek egy nap alatt átlagosan hány kontaktusa van a ![]() -edik korosztályba tartozó egyedekkel. Az A) feladatrészben
-edik korosztályba tartozó egyedekkel. Az A) feladatrészben ![]() kontaktusmátrixszal számolunk, ez a betegség megjelenése előtti normális állapot teljes populációjának kontaktusaira vonatkozik.
kontaktusmátrixszal számolunk, ez a betegség megjelenése előtti normális állapot teljes populációjának kontaktusaira vonatkozik.
A feladat során három korosztályt különböztetünk meg, fiatalokat, középkorúakat és időseket, akik egy ország lakosságának rendre negyedét, felét és negyedét teszik ki. A kontaktusmátrix (a betegség felbukkanása előtt):
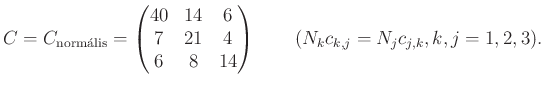
A kiindulási feltétel az, hogy a középkorú lakosság egy ezrelékében már jelen van a járvány, de másokban még nincs, és nem is volt. A két járványparaméter: ![]() és
és ![]() .
.
A differenciálegyenletek megoldását MatLab segítségével végeztem, ezen belül is az ode45 eljárással. Az ode45 nem nyílt forráskódú eljárás, a benne használt heurisztikák nem publikusak, annyi viszont biztos, hogy a megoldáshoz alapvetően negyedik és ötödik deriváltakat használ. Az ábrák megjelenítéséhez szintén MatLabot használtam. Az ábrákon szereplő időskála egysége fiktív, nem pedig nap vagy hét.
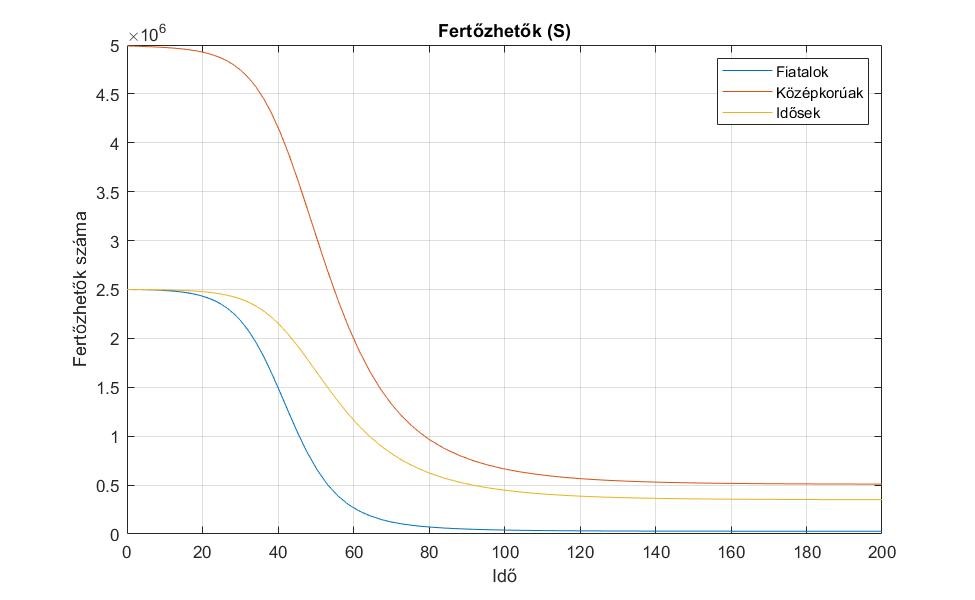
1. ábra. Az ![]() csoportok változása.
csoportok változása.
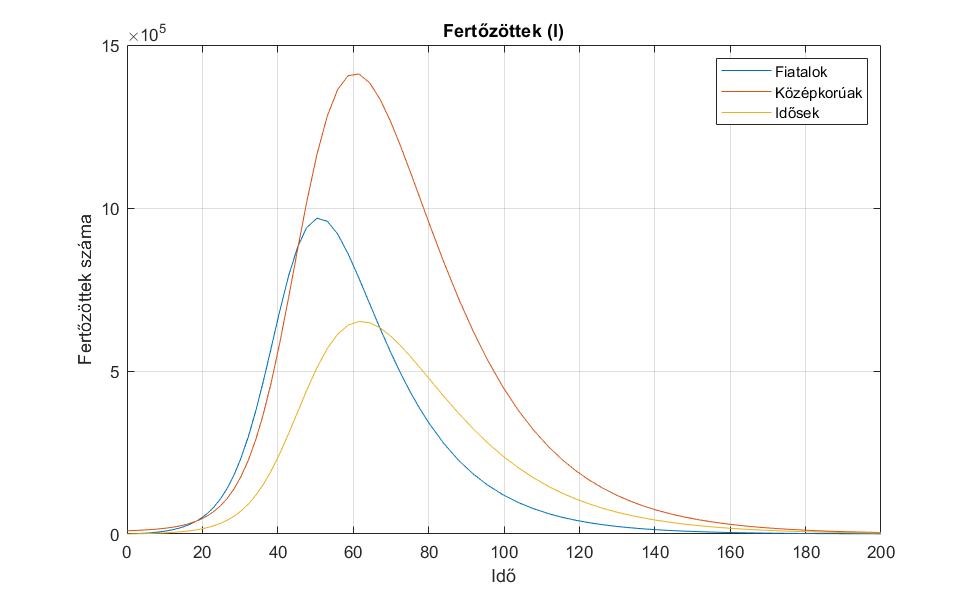
2. ábra. Az ![]() csoportok változása.
csoportok változása.
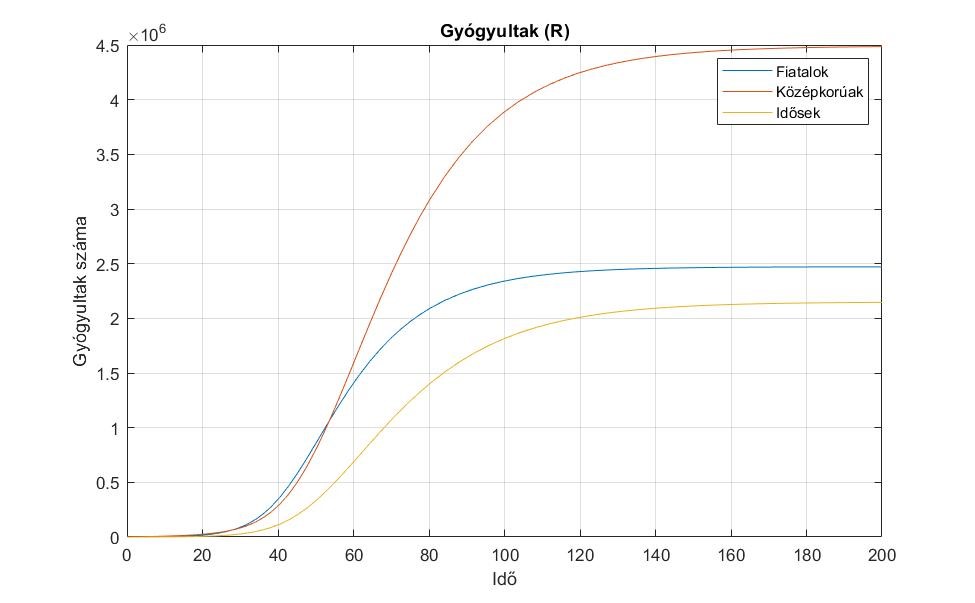
3. ábra. Az ![]() csoportok változása.
csoportok változása.
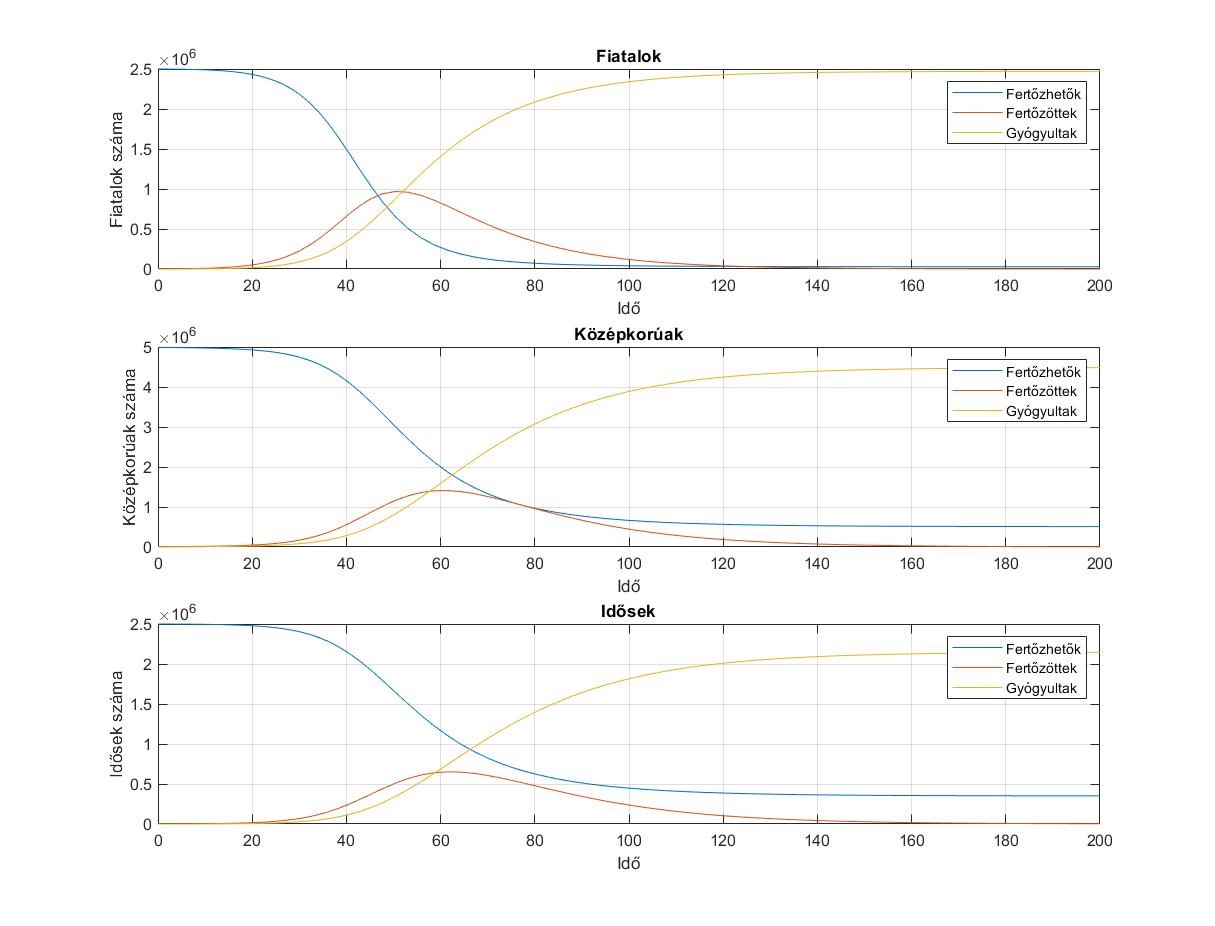
4. ábra. A járvány alakulása korosztályok szerint.
B) feladatrész
Ebben a feladatrészben bevezetünk korlátozásokat annak érdekében, hogy csökkentsük a járvány terjedésének sebességét, ezáltal ellaposítsuk a járványt. Bevezetünk egy olyan korlátozó kontaktusmátrixot ![]() , amely elviselhetővé teheti a járványt. Ennek kritériuma a
, amely elviselhetővé teheti a járványt. Ennek kritériuma a
függvény maximumának egy adott korlát alá szorítása, ez a korlát az egészségügyi ellátórendszer teherbírása. Tehát akkor tekinthetjük elviselhetőnek a járványt, ha az elviselhetőség függvényének maximuma nem haladja meg az egészségügyi ellátórendszer kapacitását. 10 milliós lakossággal számoltam. És feltételeztem, hogy az egészségügyi ellátórendszer teherbírása 2000, ennyi férőhely, működőképes lélegeztetőgép stb. található egy országban, amelyet a járványban megbetegedett emberek számára különíthetnek el. Ehhez a küszöbhöz pedig ez egy megfelelő korlátozó mátrix, amivel elviselhetővé vált a járvány, és megfelel a kritériumoknak:
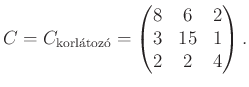
Úgy gondolom, hogy ez a kontaktusmátrix elviselhető egy járványügyi helyzetben. Ez az idős emberekkel a legszigorúbb, ami őket nehezen érintheti, de mint az alábbi képeken látható, hogy annak ellenére, hogy rájuk a legveszélyesebb, nagyon kevesen betegedhetnének meg. És így bőven jut a betegeknek kórházi ágy és megfelelő ellátás, ami elengedhetetlen ahhoz, hogy az orvosok megfelelő odafigyeléssel tudják kezelni a betegeket. Ez a korlátozás a fiatalok számára is meglehetősen szigorú, főleg a normális kontaktusmátrixhoz viszonyítva. Ez azt jelenti, hogy iskolába a megszokott módon nem mehetnek, legfeljebb csak kisebb csoportokban. A felnőttekre nézve a legmegengedőbb az általam felírt mátrix, ők kis odafigyeléssel folytathatják a napi rutinjaikat (a gazdaság érdekében). Az idősektől sokkal több odafigyelés szükséges, mivel a kór rájuk a legveszélyesebb. Nekik jelentősen csökkenteniük kell a személyes kapcsolataikat, hogy megelőzhessék a megfertőződést. Fokozott odafigyeléssel azonban szükség esetén, ha a családjuk nem tudja kisegíteni őket, elmehetnek bevásárolni.
A korlátozó kontaktusmátrixban található konkrét értékeket az előzőekben elmondott szempontok alapján próbáltam felvenni. Először az idősebbek kontaktusainak számát állítottam be. Az eredeti mátrixban a saját korosztályukkal volt a legtöbb találkozásuk és mivel nem akartam radikálisan megváltoztatni az idősebbek szokásait, így nagy csökkentéssel, de meghagytam azt, hogy ugyanúgy a saját korosztályukban lévőkkel találkozhassanak legtöbbet. Ez matematikai szempontból nem jó döntés, de az emberek beállítottsága miatt, és annak érdekében, hogy be is tartsák az intézkedéseket, úgy gondolom, hogy ezt a döntést meg kell hozni. Már volt elképzelésem a többi korosztály kontaktusainak számára is, így azok szerint próbáltam jó kompromisszumot találni az idősek és a másik két korosztály találkozására. Sajnos, ha a felnőttek dolgoznak lehetséges, hogy nem mindenki engedheti meg magának azt, hogy ne a nagyszülőket kérje meg a kisebb gyerekek gondozására (ha ők nem tudnak iskolába, óvodába menni), ezért vettem fel a fiatalabb és idősebb korosztály találkozásainak számát a duplájára, mint a középkorúak kapcsolatait az idősekkel. Ezután a középkorúak kontaktusainak számát próbáltam beállítani. Egyik elsődleges szempontom itt az volt, hogy a gazdaság és ezzel együtt az emberek jóléte érdekében fontos, hogy dolgozhassanak. Nyilván vannak akik tudnak otthonról is dolgozni, ezért csökkentettem a találkozásaik számát a saját korosztályukkal, de vásárolni nekik is el kell menniük. A többi korosztállyal történő találkozások számát is csökkentettem, de itt alapvetően a másik két korosztálytól függtek az értékek (szimmetrikus mátrix, csak a felnőttek kétszer annyian vannak a rendszerben). A fiatalokat hagytam legutoljára, mert úgy gondolom ők a legrugalmasabbak, és nincs is olyan sok kötelezettségük, főleg ha nem kell iskolába járniuk. A fiatalok esetében szóba jöhet akár kisebb csoportos foglalkozás is, ahol ez lehetséges. Az eredeti kontaktusaik számához képest őket szigorítottam meg legjobban, de úgy gondolom, hogy ez egy teljesen betartható korlátozás számukra ilyen helyzetben. A saját korosztályukkal így is sokszor találkozhatnak, a többi korosztállyal viszont csak amennyire elengedhetetlen.
A kontaktusmátrix összes elemének nullát választani szerintem nem megfelelő lépés, ugyanis ez azt jelentené, hogy senki nem találkozik senkivel (családtagok se), ami a valóságban nem kivitelezhető (persze elméletileg megoldaná a problémát).
Ha a gazdasági szempontokat is figyelembe vesszük, akkor egy olyan állapotot kell keresni, ahol nem nyúlik el nagyon a járvány, de nem is annyira gyors, hogy a megbetegedettek száma jóval az egészségügyi ellátórendszer kapacitása fölé essen. Ebből a szempontból a felnőttek korlátozása negatívan hathat a gazdaságra, így náluk érdemes lehet enyhíteni a korlátozó intézkedéseket, és a másik két korosztályt szigorítani.
Sokat próbálkoztam az eredeti megbetegedési rátával (![]() ), megemlítem evvel kapcsolatos tapasztalataimat. Amikor a megbetegedési ráta még magasabb volt sokkal szigorúbb intézkedéseket kellett bevezetni a korlátozó mátrixra, ez nyilvánvaló hiszen ez a ráta egyfajta gyorsaságot jelent. Azzal, hogy a tizenhatod részét vettük fel, már sokkal jobban ellaposítottuk a járvány terjedését. Az eredeti esetben még olyan gyors volt a járvány, hogy mindenki átesett rajta, nem volt olyan, aki nem betegedett meg (nem volt, akihez nem jutott el). Ezzel ellentétben az új megbetegedési rátával már alap esetben (korlátozások nélkül is) voltak olyanok, akik nem betegedtek meg, és így már nem meglepő, hogy sokkal enyhébb korlátozásokat lehet felvenni az új paraméter esetén. (Az eredeti megbetegedési ráta mellett közel se tudtam volna ennyire megengedő kontaktusmátrixot megadni, tízszer ekkora egészségügyi ellátórendszerrel.) Viszont érdemes foglalkozni azzal a kérdéssel, hogy mikor lehet feloldani a korlátozásokat, ha még vannak, akik nem találkoztak a betegséggel. Főleg az idősek körében lehet nagy probléma, mert a korlátozások miatt közülük sokan nem estek át a betegségen, illetve rájuk nézve a legveszélyesebb, így, ha a korlátozásokat túl gyorsan vonnánk vissza, akkor lehet, hogy sokkal súlyosabb lesz rájuk nézve a járvány utóhatása (ha még nem pusztult ki teljesen). De a többi korosztályban is jelentősen csökkent azoknak a száma, akikhez a járvány eljuthat, így nagyon fontos figyelni arra, hogy hogyan kezdjük enyhíteni a korlátozásokat. Ha túl gyorsan csináljuk, akkor akár kialakulhat egy második járványhullám is. A vakcinán kívül a másik, ami feloldhatja a járványhelyzetet, a nyájimmunitás kialakulása. Így, ha sikerül eljutni abba az állapotba, hogy a nem idős lakosság nagy része már túl van a megbetegedésen, akkor már óvatosabban ki lehetne engedni az időseket is, anélkül, hogy egy második hullámot kockáztatnánk.
), megemlítem evvel kapcsolatos tapasztalataimat. Amikor a megbetegedési ráta még magasabb volt sokkal szigorúbb intézkedéseket kellett bevezetni a korlátozó mátrixra, ez nyilvánvaló hiszen ez a ráta egyfajta gyorsaságot jelent. Azzal, hogy a tizenhatod részét vettük fel, már sokkal jobban ellaposítottuk a járvány terjedését. Az eredeti esetben még olyan gyors volt a járvány, hogy mindenki átesett rajta, nem volt olyan, aki nem betegedett meg (nem volt, akihez nem jutott el). Ezzel ellentétben az új megbetegedési rátával már alap esetben (korlátozások nélkül is) voltak olyanok, akik nem betegedtek meg, és így már nem meglepő, hogy sokkal enyhébb korlátozásokat lehet felvenni az új paraméter esetén. (Az eredeti megbetegedési ráta mellett közel se tudtam volna ennyire megengedő kontaktusmátrixot megadni, tízszer ekkora egészségügyi ellátórendszerrel.) Viszont érdemes foglalkozni azzal a kérdéssel, hogy mikor lehet feloldani a korlátozásokat, ha még vannak, akik nem találkoztak a betegséggel. Főleg az idősek körében lehet nagy probléma, mert a korlátozások miatt közülük sokan nem estek át a betegségen, illetve rájuk nézve a legveszélyesebb, így, ha a korlátozásokat túl gyorsan vonnánk vissza, akkor lehet, hogy sokkal súlyosabb lesz rájuk nézve a járvány utóhatása (ha még nem pusztult ki teljesen). De a többi korosztályban is jelentősen csökkent azoknak a száma, akikhez a járvány eljuthat, így nagyon fontos figyelni arra, hogy hogyan kezdjük enyhíteni a korlátozásokat. Ha túl gyorsan csináljuk, akkor akár kialakulhat egy második járványhullám is. A vakcinán kívül a másik, ami feloldhatja a járványhelyzetet, a nyájimmunitás kialakulása. Így, ha sikerül eljutni abba az állapotba, hogy a nem idős lakosság nagy része már túl van a megbetegedésen, akkor már óvatosabban ki lehetne engedni az időseket is, anélkül, hogy egy második hullámot kockáztatnánk.
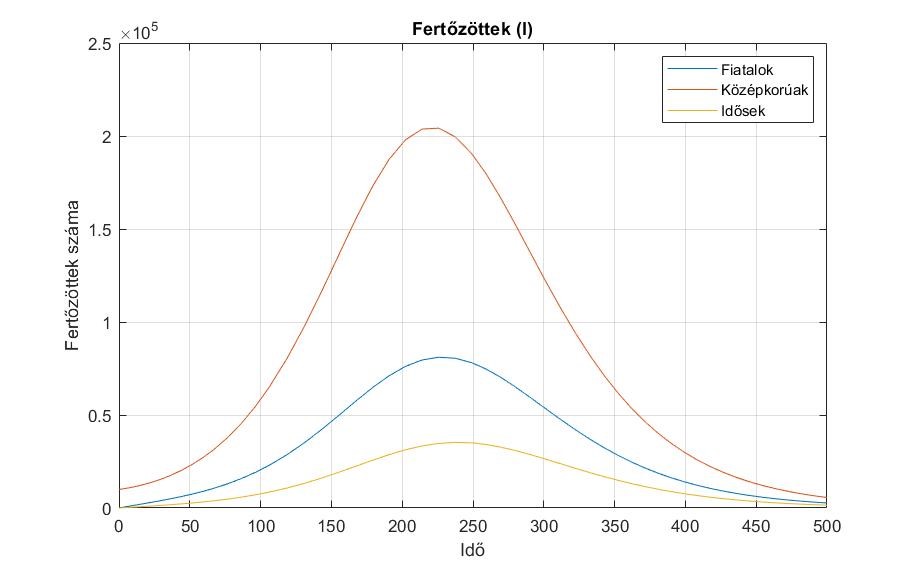
5. ábra. Az ![]() csoportok változása.
csoportok változása.
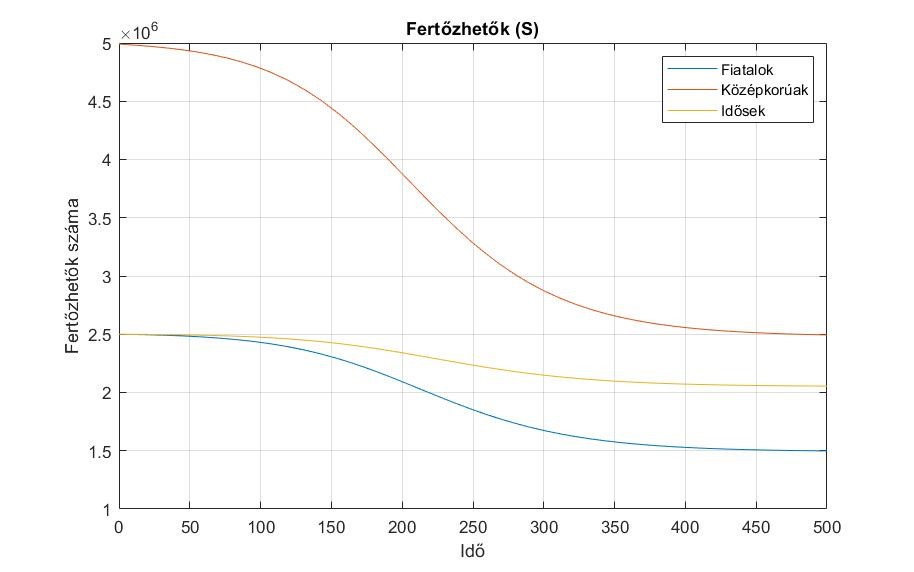
6. ábra. Az ![]() csoportok változása.
csoportok változása.
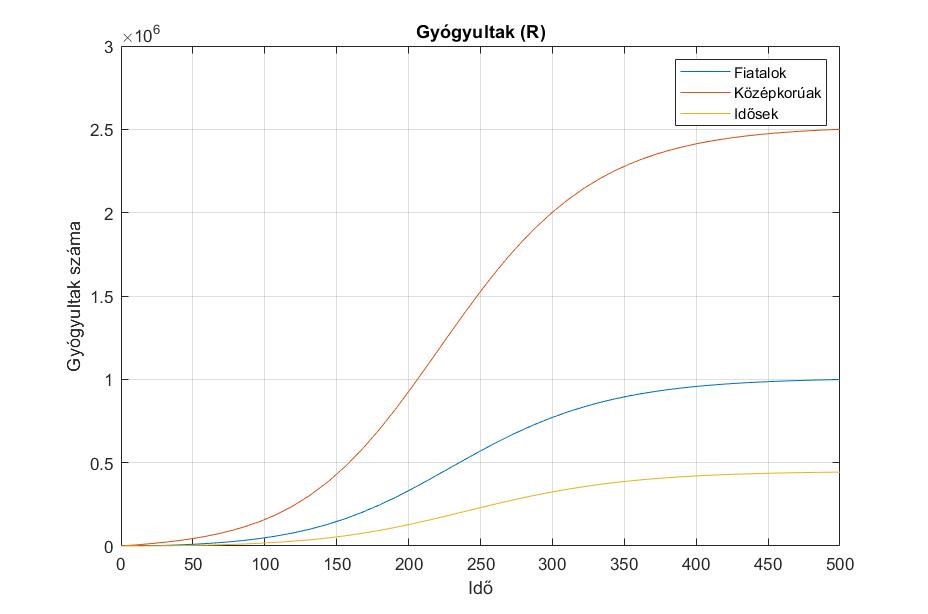
7. ábra. Az ![]() csoportok változása.
csoportok változása.
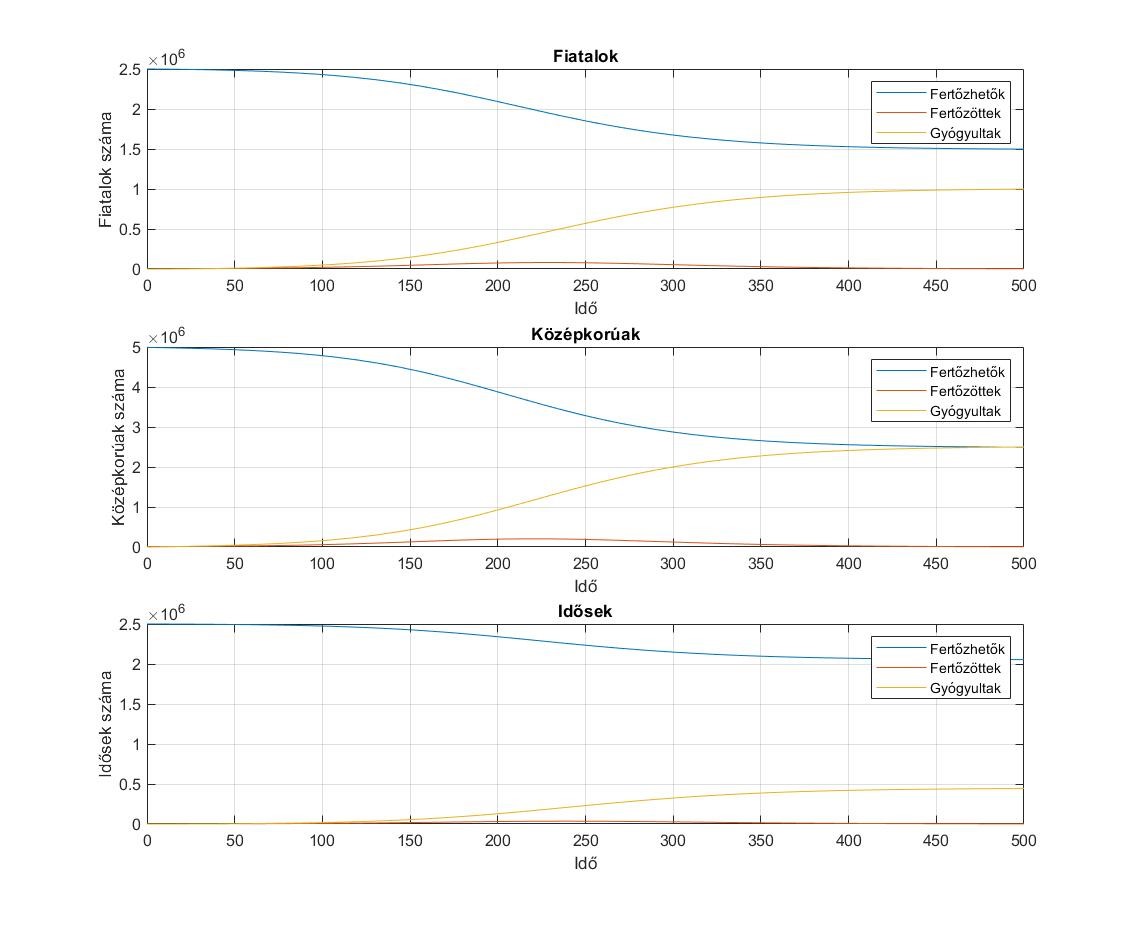
8. ábra. A járvány alakulása korosztályok szerint.
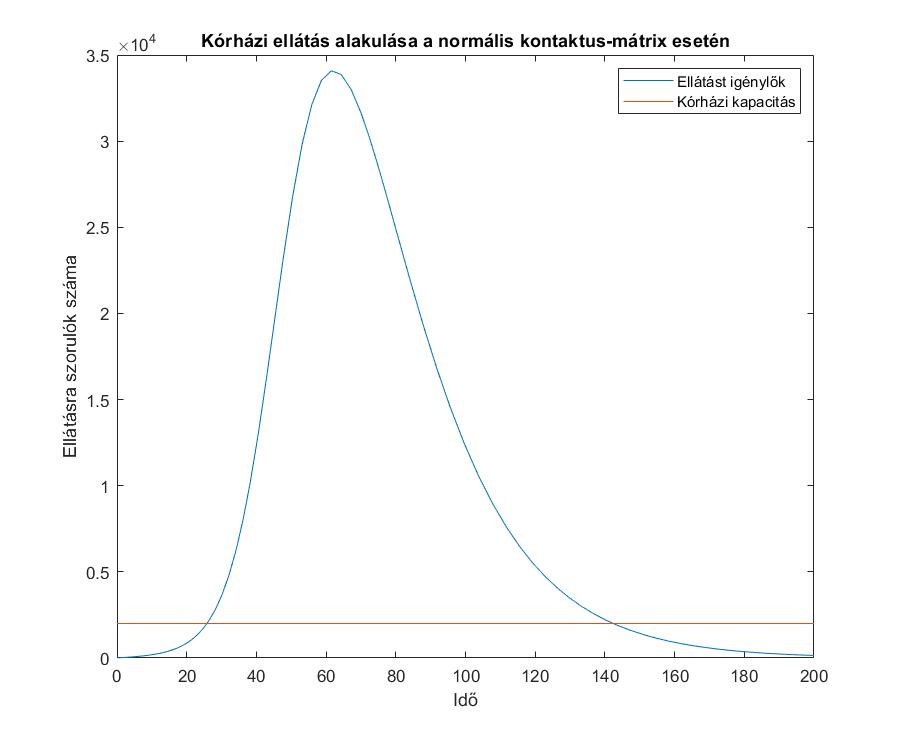
9. ábra. Kék: Az egészségügyi ellátást igénylők számának alakulása a ![]() kontaktusmátrix esetén, az ellátást igénylők
kontaktusmátrix esetén, az ellátást igénylők ![]() függvényének maximuma (
függvényének maximuma (![]() ):
): ![]() ; Barna: Az egészségügyi ellátórendszer kapacitása (2000).
; Barna: Az egészségügyi ellátórendszer kapacitása (2000).
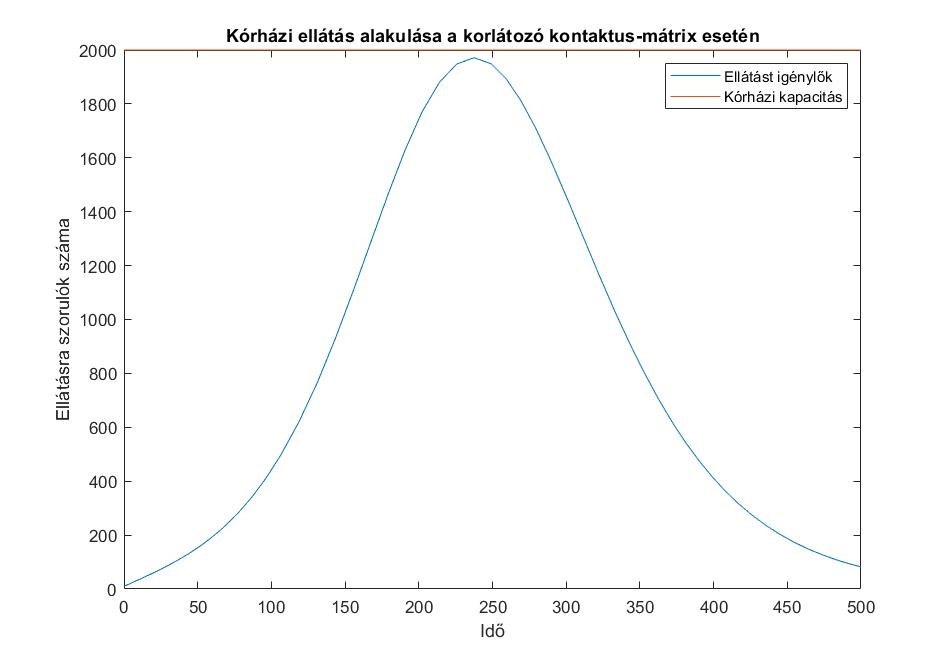
10. ábra. Kék: Az egészségügyi ellátást igénylők számának alakulása a ![]() kontaktusmátrix esetén, az ellátást igénylők
kontaktusmátrix esetén, az ellátást igénylők ![]() függvényének maximuma (
függvényének maximuma (![]() ): 1972; Barna: Az egészségügyi ellátórendszer kapacitása (2000).
): 1972; Barna: Az egészségügyi ellátórendszer kapacitása (2000).









