Mi a számsor következő tagja: 11, 8, 15, 12, 18, 28, 36, 20, 39? Bizonyára sokan emlékszünk matematikaóráinkon hasonló kérdésekre, amelyek egyik pedagógiai célja a számolási készség fejlesztése, de még hangsúlyosabban a szabályok, összefüggések felismerésére nevelés. A matematikaórákon a számsorozatokat a tanárunk állította össze oktatási céllal, ezért soha nem gondoltuk, hogy gyakorlati haszna lehet ilyen sorozatok szabályán gondolkozni. A fenti sorozat a jelenlegi járvány hazai fertőzötteinek számát tartalmazza az első néhány napon. Így mindjárt komolyabb tartalmat nyer a szabályok, összefüggések felismerésének készsége.
Íme néhány más sorozat:
123, 172, 472, 970, 1424, 1535, az okostelefon-eladások millió darabban 2007-től két évenként,
623, 907, 1608, 3018, 4448, 6134, Földünk lakossága millió főben 1700-tól száz évenként,
650, 150, 90, 54, egy antibiotikum mennyisége a vérben milligrammban a gyógyszer bevétele után óránként,
végül 8550, 8640, 8740, 8730, 8750, 8770, 8780, az OTP részvény árfolyama forintban 2017 március 16-án óránként.
Bármelyik sorozat esetében sokan sokat adnának azért, hogy a sorozat következő néhány tagját előre meg tudják mondani. Iskolai emlékeink alapján azt gondoljuk, hogy pusztán a sorozat számainak hosszas „nézegetésével” fel lehet ismerni valami „misztikus” szabályt, amivel a további tagok kiszámolhatók. A matematika azonban ennél összetettebb módszereket dolgozott ki az elmúlt néhány száz év során. Most a járvány foglalkoztat mindnyájunkat, így az első sorozat kapcsán mutatunk be néhány gondolatot arról, hogy a modern matematikai gondolkozás hogyan közelít meg ilyen kérdéseket.
Matematikai modell
Európában a XVII. századra érett meg az áttörés a fizikai folyamatok matematikai modellezése terén, biztos sokan hallottunk Newton almájáról, vagy Galilei kísérletéről a pisai ferde toronyban. Ekkor fedezték fel (egyesek szerint inkább kitalálták) a differenciál- és integrálszámítást (összefoglaló néven kalkulust) elsősorban a fizikai folyamatok leírását lehetővé tevő differenciálegyenletek bevezetése céljából. Ezek olyan egyenletek, amelyekben az ismeretlen nem egy szám, hanem egy függvény, például a toronyból leejtett tárgy helye az idő függvényében, vagy a Föld pályája a Nap körül, hogy az előbbi két tudós kutatásaihoz kapcsolódjunk. A matematika érettségi anyaga a legtöbbek számára a XVII. századi matematika előtt véget ér, néhányan mégis találkoznak a kalkulus elemeivel, ami a természettudományi, mérnöki, informatikai, gazdasági egyetemi képzések bevezető matematika anyagának alapja. A bevezetésben említett számsorok megfejtése differenciálegyenleteken alapszik. Egy híres mondás szerint a matematika megértéséhez „nincs királyi út”.1 Az egymásra épülő fogalmak és módszerek megismerése fokozatosan történik az iskolában tanult matematikai készségekből kiindulva, a különböző matematikai módszerek (pl. a fent említett kalkulus) használatának elsajátításán keresztül az elvont fogalmak kiépítéséig. Ezeken a lépcsőkön egyre kevesebb embernek van kapacitása, ideje, energiája végigmenni, és egyre kevesebben engedhetik maguknak, hogy a matematika szépségének és mélységének hódoljanak, így a matematikus mire doktorál, egy elég szűk családban találja magát. Amikor a szűk matematikus családon kívül valaki érdeklődik a fenti számsor következő néhány tagja iránt, akkor nehéz dolga van a matematikusnak még akkor is, ha vannak eszközei a számok előrejelzésére. Most mégis megpróbálkozunk néhány szerény lépést tenni ezen az úton, bízva az olvasó kitartásában.
A járványterjedés matematikai modellezése
A már említett XVII. századi áttörés óta a fenti típusú számsorok megfejtésének általános kiindulási pontja egy modell létrehozása, ami valójában egy matematikai struktúra, nem a valóság pontos mása. Nézzük, hogy a járványterjedés modellezése milyen alapgondolatból indul el. A XX. század elején kidolgozott modell az egyedeket néhány csoportra osztja a fertőzés állapota szerint. A legegyszerűbb modell három csoportot különböztet meg: fogékonyak (jele ![]() az angol susceptible szóból), fertőzők (
az angol susceptible szóból), fertőzők (![]() , infectious) és gyógyultak (
, infectious) és gyógyultak (![]() , recovered vagy removed). A járvány terjedése előtt az összes egyed fogékony, és a járvány néhány fertőző egyed megjelenésével kezdődik. A kérdés, hogy egy későbbi időpontban mennyi a fertőzöttek száma. Ekkor kerül a képbe a differenciálegyenlet, ami a folyamatot modellezi, azaz összefüggést ad az
, recovered vagy removed). A járvány terjedése előtt az összes egyed fogékony, és a járvány néhány fertőző egyed megjelenésével kezdődik. A kérdés, hogy egy későbbi időpontban mennyi a fertőzöttek száma. Ekkor kerül a képbe a differenciálegyenlet, ami a folyamatot modellezi, azaz összefüggést ad az ![]() ,
, ![]() és
és ![]() megváltozása és ezek aktuális értéke között. Például egy egyszerű modellfeltevés, hogy az
megváltozása és ezek aktuális értéke között. Például egy egyszerű modellfeltevés, hogy az ![]() növekedése arányos az
növekedése arányos az ![]() mennyiségével. Az adatok mutatják meg, hogy ez a feltevés helytálló-e, illetve azokból határozható meg, hogy mekkora az arányossági tényező. Az elszánt Olvasó kedvéért bemutatjuk a három változóra vonatkozó legegyszerűbb differenciálegyenleteket, azaz a legegyszerűbb matematikai modellt.
mennyiségével. Az adatok mutatják meg, hogy ez a feltevés helytálló-e, illetve azokból határozható meg, hogy mekkora az arányossági tényező. Az elszánt Olvasó kedvéért bemutatjuk a három változóra vonatkozó legegyszerűbb differenciálegyenleteket, azaz a legegyszerűbb matematikai modellt.
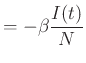 |
|
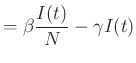 |
|
Ebben a pont jelenti az idő szerinti deriválást, ![]() a populáció egyedszáma,
a populáció egyedszáma, ![]() az úgynevezett fertőzési ráta,
az úgynevezett fertőzési ráta, ![]() pedig a gyógyulási ráta. Az egyenlet kifejezi, hogy az
pedig a gyógyulási ráta. Az egyenlet kifejezi, hogy az ![]() állapotból az egyedek az
állapotból az egyedek az ![]() -be, az
-be, az ![]() -ből pedig az
-ből pedig az ![]() -be kerülhetnek az egyenletekben szereplő rátákkal. Sajnos az egyenletek megoldásának elemzése a „nincs királyi út” kategóriába esik, így ebben az írásban elrejtve marad az olvasó előtt. Az eredményt viszont meg tudjuk mutatni az 1. ábrán.
-be kerülhetnek az egyenletekben szereplő rátákkal. Sajnos az egyenletek megoldásának elemzése a „nincs királyi út” kategóriába esik, így ebben az írásban elrejtve marad az olvasó előtt. Az eredményt viszont meg tudjuk mutatni az 1. ábrán.
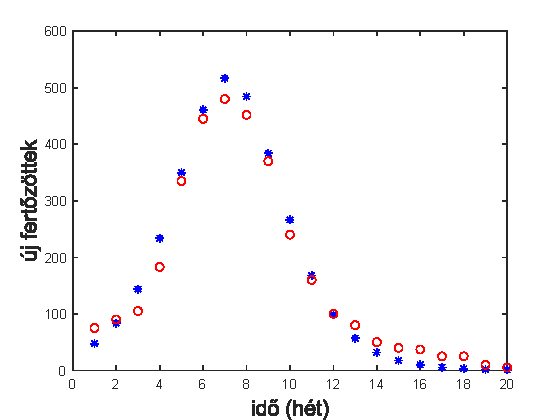
1. ábra. A 2016-os hazai influenzajárvány új fertőzötteinek száma hetente (piros körök), valamint a modellből kapott értékek (kék csillagok).
Ezen a 2016-os hazai influenzajárvány adatai látszanak (piros körökkel), valamint a modellből kapott értékek (kék csillagok). A vízszintes tengelyen az idő látszik hetekben a járvány januári indulásától számolva, a függőleges tengelyen pedig a hetente jelentett új fertőzöttek száma 100 ezer főre vetítve (tehát a teljes hazai népességben ez a szám százszor ekkora). A modell valamennyire jó közelítést ad a járvány folyamatáról, de láthatjuk, hogy nem tud minden adatot pontosan visszaadni. Elsőként figyeljük meg, hogy a fertőzöttek száma emelkedik egy darabig, majd csökkenni kezd és nagyjából 20 hét alatt a járvány véget ért. Az ![]() értékét is ábrázolva láthatjuk, hogy hányan estek át a betegségen a járvány teljes lefolyása során. Erre itt kb. 3400-at kapunk, az említett 100 ezer főre vetítve, azaz nagyjából a lakosság 3,4 százaléka esett át abban az évben az influenzán (legalábbis a hivatalos orvosi bejelentések alapján).
értékét is ábrázolva láthatjuk, hogy hányan estek át a betegségen a járvány teljes lefolyása során. Erre itt kb. 3400-at kapunk, az említett 100 ezer főre vetítve, azaz nagyjából a lakosság 3,4 százaléka esett át abban az évben az influenzán (legalábbis a hivatalos orvosi bejelentések alapján).
Mire következtethetünk a matematikai modell segítségével?
A járvány terjedése során három fontos fogalmat szoktak emlegetni, melyeket a matematikai modellek segítségével lehet precízen értelmezni:
![]() alap reprodukciós szám
alap reprodukciós szám ![]() ,
,
![]() a fertőzöttek maximális száma
a fertőzöttek maximális száma ![]() ,
,
![]() a fertőzésen átesettek száma
a fertőzésen átesettek száma ![]() .
.
Nézzük mit jelentenek ezek, és a modellből hogyan határozhatók meg. Az alap reprodukciós szám, ![]() , azt mutatja meg, hogy a járvány kezdetén egy beteg átlagosan hány egészséges egyedet fertőz meg. A differenciálegyenletekből az analízis egyszerű eszközeivel levezethető, hogy
, azt mutatja meg, hogy a járvány kezdetén egy beteg átlagosan hány egészséges egyedet fertőz meg. A differenciálegyenletekből az analízis egyszerű eszközeivel levezethető, hogy
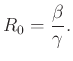
Az 1. ábrán bemutatott görbén látható, hogy az ![]() függvénynek egy maximuma van. Ez nemcsak a konkrét példában van így, hanem általánosan is igazolható. A függvény maximum értékét jelöli
függvénynek egy maximuma van. Ez nemcsak a konkrét példában van így, hanem általánosan is igazolható. A függvény maximum értékét jelöli ![]() . Ez mutatja, hogy az egészségügyi ellátórendszert érő legnagyobb terhelés mekkora, azaz legfeljebb hány ember lesz a járvány folyamán egyszerre az
. Ez mutatja, hogy az egészségügyi ellátórendszert érő legnagyobb terhelés mekkora, azaz legfeljebb hány ember lesz a járvány folyamán egyszerre az ![]() kategóriában. Szintén egyszerű számolás mutatja, hogy
kategóriában. Szintén egyszerű számolás mutatja, hogy
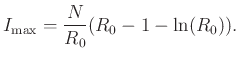
Végül a fertőzésen átesettek száma az ![]() függvény értéke a járvány lefolyása végére (amikor
függvény értéke a járvány lefolyása végére (amikor ![]() értéke visszatér nullára). Mivel a járvány lefolyásának idejét nem ismerjük, ennek precíz definíciója: az
értéke visszatér nullára). Mivel a járvány lefolyásának idejét nem ismerjük, ennek precíz definíciója: az ![]() függvény határértéke
függvény határértéke ![]() tart végtelen esetén, amit
tart végtelen esetén, amit ![]() jelöl. Az előbbieknél kicsit bonyolultabb számolással levezethető, hogy az
jelöl. Az előbbieknél kicsit bonyolultabb számolással levezethető, hogy az ![]() arány teljesíti az
arány teljesíti az
transzcendens egyenletet. Ennek numerikus megoldása egyszerű feladat, így az ![]() ,
, ![]() és
és ![]() paraméterek ismeretében könnyen meg lehet mondani, hogy hányan fognak átesni összesen a fertőzésen.
paraméterek ismeretében könnyen meg lehet mondani, hogy hányan fognak átesni összesen a fertőzésen.
E három fontos járványtani mennyiség összefüggése világos az egyenletekből. Az ![]() értéke meghatározza a másik kettőt. A járvány elleni védekezés fontos módja az egyedek elszigetelése (karantén), azaz a
értéke meghatározza a másik kettőt. A járvány elleni védekezés fontos módja az egyedek elszigetelése (karantén), azaz a ![]() és ezáltal az
és ezáltal az ![]() csökkentése. Láthatjuk, hogy ezzel csökken az
csökkentése. Láthatjuk, hogy ezzel csökken az ![]() , vagyis az egészségügyi ellátórendszer terhelése, viszont ezzel együtt az
, vagyis az egészségügyi ellátórendszer terhelése, viszont ezzel együtt az ![]() is, azaz nem alakul ki a nyájimmunitás, a társadalom széles védettsége. A két mennyiség kapcsolatát mutatja a 2. ábra. A vízszintes tengelyen az
is, azaz nem alakul ki a nyájimmunitás, a társadalom széles védettsége. A két mennyiség kapcsolatát mutatja a 2. ábra. A vízszintes tengelyen az ![]() arány, a függőlegesen pedig az
arány, a függőlegesen pedig az ![]() arány van feltüntetve. Ez mutatja például, hogy ha a nyájimmunitáshoz a társadalom 80 százalékának kell átesnie a fertőzésen (azaz
arány van feltüntetve. Ez mutatja például, hogy ha a nyájimmunitáshoz a társadalom 80 százalékának kell átesnie a fertőzésen (azaz ![]() ), akkor a járvány legrosszabb időszakában a társadalom kb. 15 százaléka beteg (azaz
), akkor a járvány legrosszabb időszakában a társadalom kb. 15 százaléka beteg (azaz ![]() ).
).
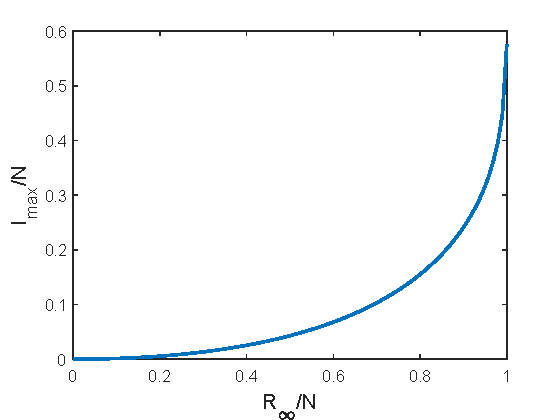
2. ábra. Az ![]() és
és ![]() arányok kapcsolata a legegyszerűbb SIR matematikai modellben.
arányok kapcsolata a legegyszerűbb SIR matematikai modellben.
A modell általánosításai
A modell általánosítását a valósággal való összehasonlítás motiválja. Nézzük meg az 1. ábra alapján a modell pontatlanságából eredő következtetéseket. Azt láthatjuk, hogy az első hetekben a modell nagyobb fertőzöttséget jelez, mint az adatok. Másképp nézve, ha valaki ez első néhány hét adatai alapján határozná meg a modell paramétereit, akkor kisebb járványt jósolna. Ez arra sarkallja az epidemiológiai szakembereket, és a matematikusokat, hogy pontosabb modellt készítsenek. A pontosabb modell rendszerint több csoportra osztja a társadalmat, például korosztályokat hoz létre az S, I és R kategóriákon belül, vagy terület szerint is felbontja a teljes populációt kisebb részekre. (Lásd pl. ebben a számban Garay Barnabás és Molnár Zsófia cikkét.) Ezek a modellek már több egyenletből állnak (ezért tudnak pontosabb előrejelzést adni), viszont emiatt több paramétert is tartalmaznak, amelyeket az adatokból nem könnyű pontosan meghatározni. A legrészletesebb modell a társadalom minden egyes tagját külön kezeli, és valamilyen módon az emberek közötti kapcsolatokat is figyelembe veszi, ezért hálózati modellnek is nevezik, és a hálózattudomány modern eszköztárán alapszik. (A járványterjedés hálózatelméleti megközelítéséről szól a szerző nemrégiben megjelent könyve: [1]).
A jelenlegi járvány leírására is már számtalan modell született, és sokan sokféle módon próbálják előre jelezni a járvány lefolyását, valamint segíteni a döntéshozókat. A hazai stratégia a járványgörbe ún. ellaposítása, ami azt jelenti, hogy a fenti görbe maximuma ne érjen el olyan nagy értéket, ami túlterheli az egészségügyi ellátórendszert. A görbét a modellben szereplő paraméterek módosításával tudjuk befolyásolni, amint azt az előbb a legegyszerűbb modell esetében megvizsgáltuk és a 2. ábrán bemutattuk. Természetesen az összetett modellekben nem egyetlen paraméter szerepel (mint fent az ![]() volt), hiszen a fertőzési ráta különbözhet korosztályonként és területenként, de akár munkahelyenként is. A mostani kutatások tárgya éppen az, hogy ezek a modellek mennyire illeszkednek jól az adatokhoz, és a folyamat irányításában hogyan használhatók, milyen korlátozások bevezetését mutatják leghatékonyabbnak. Ezeken felül, ha az oltóanyag elkészül, akkor annak eldöntésében is segítenek, hogy a társadalom mely csoportjait milyen sorrendben célszerű beoltani, hogy minél hamarabb visszatérhessen az élet a megszokott kerékvágásba. A kérdések látszólag egyszerűek, azonban az egyre összetettebb modellek létrehozása és vizsgálata számos kutatónak jelent kihívást.
volt), hiszen a fertőzési ráta különbözhet korosztályonként és területenként, de akár munkahelyenként is. A mostani kutatások tárgya éppen az, hogy ezek a modellek mennyire illeszkednek jól az adatokhoz, és a folyamat irányításában hogyan használhatók, milyen korlátozások bevezetését mutatják leghatékonyabbnak. Ezeken felül, ha az oltóanyag elkészül, akkor annak eldöntésében is segítenek, hogy a társadalom mely csoportjait milyen sorrendben célszerű beoltani, hogy minél hamarabb visszatérhessen az élet a megszokott kerékvágásba. A kérdések látszólag egyszerűek, azonban az egyre összetettebb modellek létrehozása és vizsgálata számos kutatónak jelent kihívást.
Zárógondolat
Végezetül visszatérve a bevezetésben mutatott számsorozatokhoz, mindegyikhez tartozik egy-egy matematikai modell, amely segít a folyamat megértésében, előrejelzésében és irányításában. Ezzel matematikusok ezreinek, akik 5 év egyetemi képzés során végigjárták a fent említett lépcsőket, munkát adva. Mai, technológiai társadalmunk működése így elképzelhetetlen az összetett matematikai modellek használata nélkül. (Érdekes írás ezzel kapcsolatban [2]).
Nem csoda tehát, hogy a matematika szakot végzett hallgatók annyira könnyen el tudnak helyezkedni kiváló munkahelyeken. Örömmel látjuk, hogy ennek híre van a pályaválasztó fiatalok között, idén több mint 10 százalékkal nőtt az ELTE matematika alapszakára első helyen jelentkezett hallgatók száma.
Irodalomjegyzék
[1] https://www.springer.com/gp/book/9783319508047
[2] http://fortune.com/2015/01/22/the-algorithmic-ceo/-
Numerikus analízis és nagy hálózatok MTA-ELTE Kutatócsoport
Lábjegyzet
- 1
- A legenda szerint I. Ptolemaiosz egyiptomi király megkérdezte Euklidészt, hogy nincs-e rövidebb és könnyebb módja a geometria megértésének annál, mint amit Euklidész az Elemek című művében leírt. Erre felelte Euklidész azt, hogy „A geometriához nem vezet királyi út”.









