2020 első hónapjaiban világszerte nagy riadalmat okoz a kínai Vuhanból kiindult új koronavírus-járvány, amely (március 3-i adatok szerint) már több mint 91 ezer embert fertőzött meg és 3118 halálos áldozatot követelt. A járvány 2019 decemberében indult az első tüdőgyulladásos esetek megjelenésével, a betegség legfőbb tünetei a láz és légzési nehézségek. A betegség gyors terjedésére a kínai hatóságok számos intézkedéssel reagáltak: január 23-án Vuhant és a környező városokat karantén alá helyezték, új kórházak építését kezdték meg, Kína-szerte lezárták a legfontosabb idegenforgalmi látványosságokat, számos légitársaság törölte kínai járatait. Az intézkedések ellenére a betegség hamar átterjedt más országokra: március elejéig már 77 országban jelent meg, és sok helyen – pl. Olaszországban, Dél-Koreában, Iránban – terjedni is kezdett. Az orvosok, epidemiológusok mellett a matematikusok is hamar vizsgálni kezdték a betegség terjedését. De hogyan segíthet a matematika a járványterjedés megértésében? Sokak számára meglepő lehet, de a matematikai modellek alkalmazása igen hatékony módszer lehet a járványok elleni küzdelemben. Ahogy a WHO (Egészségügyi Világszervezet) is hangsúlyozta február 19-i helyzetjelentésében, az elérhető epidemiológiai és klinikai adatok leíró statisztikai elemzése mellett nagyon fontosak a korszerű matematikai modellek, hiszen segítségükkel pontosabb becsléseket adhatunk a COVID-19 járvány fő paramétereire – mint az inkubációs időszak és a fertőző időszak hossza, vagy a járvány reprodukciós száma –, előre jelezhetjük a járvány jövőbeli terjedését, kiértékelhetjük az eddigi intézkedések hatását, esetleg új intézkedéseket javasolhatunk. A WHO szorosan együttműködik a matematikai modellezők nemzetközi közösségével. Fontos kiemelnünk, hogy bár a járványok matematikai modellezése hosszú múltra tekint vissza, az elmúlt évtizedekben – amellett, hogy az orvosi kutatások eredményeként a patogénekről és az immunrendszerről is sokkal többet tudunk –, az epidemiológiai adatok is sokkal nagyobb mennyiségben és részletességben állnak rendelkezésre, továbbá a számítógépek is sokkal hatékonyabban, gyorsabban végzik a szimulációkat, ami lehetővé teszi, hogy egyre összetettebb és a valóságot egyre pontosabban leíró matematikai modelleket adjunk a járványok terjedésére.
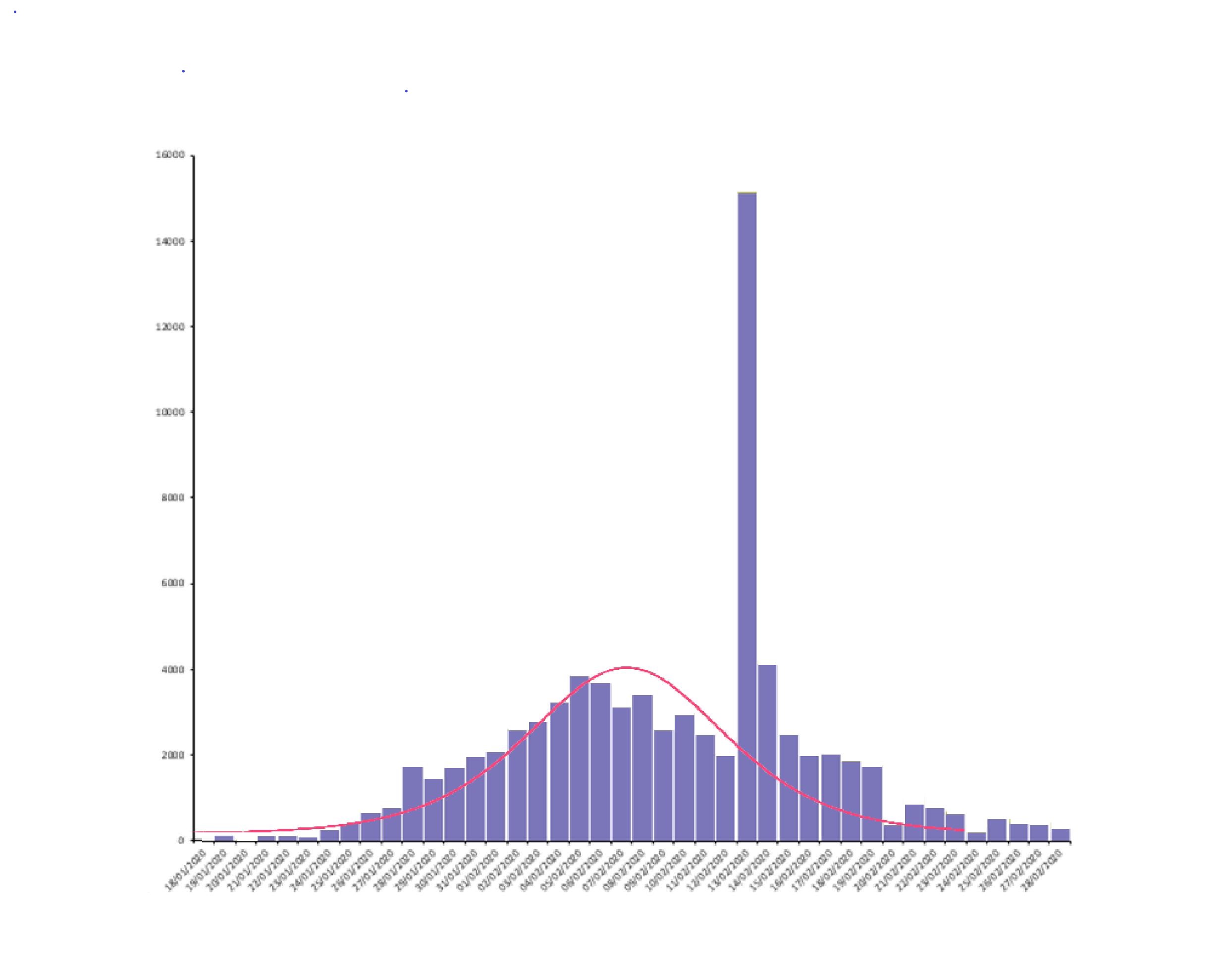
A kínai koronavírusos esetek száma és egy egyszerű matematikai járványtani modell egy megoldása. A kiugró esetszámokat jelző oszlopok annak eredményeként jöttek létre, hogy új módszert vezettek be a koronavírusos esetek regisztrálására.
A Szegedi Tudományegyetem Bolyai Intézetének hat matematikusa – Boldog Péter, Tekeli Tamás, Vizi Zsolt, Dénes Attila, Bartha Ferenc és Röst Gergely – azt modellezte, hogy az egyes országokban mekkora a veszélye egy Kínán kívüli járványkitörésnek.
A szegedi kutatók egy háromfázisú modellt alkottak meg. Elsőként egy differenciálegyenlet-rendszer segítségével adtak becslést az összes (a karanténnal lezárt Hubei tartományon kívüli) kínai eset várható számára. Fontos kiemelni, hogy a modell nemautonóm, vagyis időfüggő paramétert is tartalmaz, a kutatók ugyanis figyelembe vették a kínai hatóságok intézkedéseit, azt feltételezve, hogy a növekvő mértékű beavatkozások az idő múlásával egyre hatékonyabban fékezik a járvány terjedését. A betegek számának becslésére felhasználták a betegség reprodukciós számára (vagyis az egy beteg által generált új fertőzések várható értékére) és a betegség egyéb paramétereire (inkubációs és fertőző periódus átlagos hossza) elérhető adatokat: a lappangási időre 5,1 napos, a reprodukciós számra 2,6-es, a fertőző időszakra 3,3 napos becslést használtak. A kutatók figyelembe vették azt is, hogy a betegek valódi száma aluljelentés miatt jelentősen eltérhet a valódi esetszámtól.
A modell második részében a differenciálegyenletes modell segítségével kapott betegszámot alkalmazták egy individuális alapú, globális mobilitási modellben, hogy – a nemzetközi légiforgalmi adatok alapján, az utazási megszorítások figyelembevételével – becslést adjanak arra, hogy hány fertőzött utazó érkezhet Kínán kívüli célállomásokra.
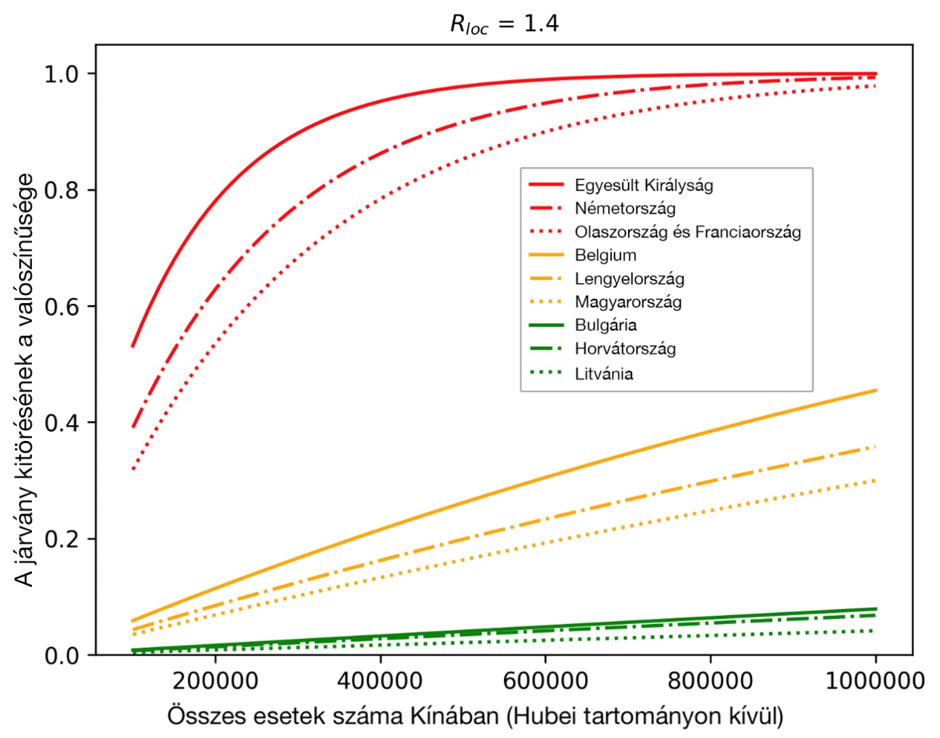
Nem minden beteg okoz azonban járványt a célországban, hiszen többek között az adott beteg fertőzőképességétől, kontaktszámától is függ, hogy ez a beteg hány újabb fertőzést generál. A modell harmadik fázisa egy ún. elágazó sztochasztikus folyamat, amelynek segítségével leírható a betegség terjedése a célországban a kezdeti időszakban, és kiszámítható egy járvány kitörésének valószínűsége. A kutatók kiszámolták annak a valószínűségét, hogy egy beteg által indított elágazó folyamat kihal. Ha feltesszük, hogy i beteg érkezett Kínából, egy járvány kitörésének valószínűségét annak a valószínűsége adja, hogy az i beteg által indított elágazó folyamatok közül nem mindegyik hal ki. A modell segítségével a kutatók megállapították, hogy a járványkitörés veszélye hogyan függ a három kulcsparamétertől: a kínai esetek számától, a célország és Kína közti közlekedési kapcsolatoktól, azaz az járatok és utasok számától, a járatok számának csökkentésétől és a célállomáson végzett szűréstől, valamint a célországbeli intézkedések eredményességétől. Az eredmények azt mutatják, hogy a Kínával kevésbé szoros összeköttetésben álló, de viszonylag magas helyi reprodukciós számmal rendelkező országokban elsősorban a beérkező utazók szűrésével, valamint a közlekedési kapcsolatok csökkentésével mérsékelhető a járványkitörés kockázata. A Kínával szoros összeköttetésben álló, de alacsonyabb helyi reprodukciós számmal rendelkező országokban a helyi reprodukciós szám további csökkentése a leginkább hatékony intézkedés. A két tényező szempontjából közepes érintettségű országokban mindezen intézkedések kombinálásával érhető el a legjobb eredmény.
A modellel különböző ázsiai, amerikai és európai országcsoportok kockázatait is összehasonlították, ez alapján Magyarország a viszonylag alacsony kockázatú országok közé tartozik. A modell alapján született eredményeket bemutató cikk megjelenése óta a korábban a legmagasabb kockázatú európai országok egyikeként megjelölt Olaszországban is súlyos járvány tört ki, illetve más, nagy kockázatú országok – Németország és Franciaország – is a legnagyobb esetszámú országok között vannak. A modell alapján az is látható volt, hogy amikor Iránban hivatalosan még csak 28 esetről lehetett tudni, a valóságban több ezer eset lehetett már akkor. Erről a népszerű tudományos magazin, a New Scientist is beszámolt. Az új járványgócok megjelenésével, a kínai terjedés csökkenésével a modellben leírt szituáció jelentősen megváltozott, így a kutatók új modellek megalkotásával, vizsgálatával folytatják a munkát.
A szegedi matematikusok tanulmánya a Journal of Clinical Medicine folyóiratban jelent meg, munkájukról további részletek olvashatók az alábbi oldalon: http://www.math.u-szeged.hu/~rost/Coronavirus/COVID19.html
Boldog, Péter; Tekeli, Tamás; Vizi, Zsolt; Dénes, Attila; Bartha, Ferenc; Röst, Gergely
Risk Assessment of Novel Coronavirus COVID-19 Outbreaks Outside China
Journal of Clinical Medicine, 2020, 9, 571
https://www.mdpi.com/2077-0383/9/2/571
Köszönetnyilvánítás
A cikk az Emberi Erőforrások Minisztériuma ÚNKP-19-4 Kódszámú Új Nemzeti Kiválóság Programjának támogatásával készült.
Dénes Attila
tudományos munkatárs, SZTE Bolyai Intézet









