2019 decemberében a Szegedi Tudományegyetem Bolyai Intézetének vendége volt Philip Maini, az Oxfordi Egyetem professzora, a matematika biológiai alkalmazásainak világszerte egyik legnevesebb kutatója. Maini professzor Oxfordban végzett egyetemi tanulmányait követően Oxfordban és a Utahi Egyetemen is dolgozott, 1998 óta az Oxfordi Egyetem Wolfson Matematikai Biológiai Központjának igazgatója, Maini professzor kutatási területei közé tartozik a daganatok, a sebgyógyulás és az embrionális mintaképződés matematikai modellezése. Philip Maini amellett, hogy a Bolyai Intézet biomatematikai szemináriumának keretein belül a fiatal kutatók részére beszámolt a matematikai biológia területén végzett kutatással kapcsolatos tapasztalatairól, a Bolyai Intézet hagyományos karácsonyi szemináriumán is előadást tartott A biológiai és kémiai önszerveződés matematikája címmel.
 Philip Maini előadása a Bolyai Intézet karácsonyi szemináriumán
Philip Maini előadása a Bolyai Intézet karácsonyi szemináriumán
Előadásában elsőként az állatok mintaképződéséről beszélt. Az ezzel kapcsolatos első matematikai modellek az elsősorban a számítástudomány területén elért eredményeiről és az Enigma feltöréséről ismert Alan Turing nevéhez fűződnek. Turing 1952-ben jelentette meg A morfogenezis kémiai alapjai című, a természetes minták képződésére vonatkozó elméletét leíró cikkét, melyben azt a gondolatot vetette fel, hogy a biológiai mintázatok egymással reagáló és diffundáló kémiai anyagok (morfogének) hatására alakulhatnak ki. Elmélete szerint kémiai anyagok rendszere, amely diffúzió nélkül stabil állapotba áll be, instabillá válik a diffúzió következtében. Ez első hallásra hihetetlenül hangzik, hiszen a diffúzió (részecskék véletlenszerű áramlása) általában megszünteti a mintázatokat, gondoljunk csak egy vízbe ejtett tintacseppre.Turing elméletének matematikai alátámasztására egy olyan egyenletet alkalmazott, amelyet a matematikusok reakció-diffúzió egyenletnek hívnak. A rendszer reakciót leíró részének van egy stabil egyensúlyi állapota, amely a teljes reakció-diffúzió rendszerben instabillá válik.
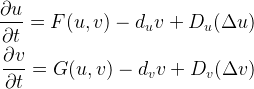
Reakció-diffúzió-egyenlet
A rendszer működését Maini professzor egy égő mezővel vont párhuzammal tette érthetővé: képzeljünk el egy mezőt, ahol tűz ég. Az égő tűz felforrósítja a füvet, meggyullad, vagyis a tűz önmagát aktiválja. A tűz azonban a mezőn élő szöcskéket is aktiválja, amelyek erősen izzadni kezdenek. Az izzadságuk akadályozza a tüzet (vagyis inhibitorként működik). Ha a tűz gyorsabban terjed, mint ahogy a szöcskék mozognak, az egész mező kiégett feketeséggé változik. Ha azonban a szöcskék gyorsabban ugranak, mint ahogy a tűz terjed, izzadságukkal megnedvesítenek bizonyos területeket, amelyekre nem tud átterjedni a tűz. Így végül a fekete mezőt zöld szigetek tarkítják, vagyis mintázat alakul ki.
 Turing-mintázatok
Turing-mintázatok
Forrás: https://en.wikipedia.org/wiki/Turing_pattern#/media/File:TuringPattern.PNG
A mintázat kialakulására rendelkezése álló felület nagysága fontos a mintázat bonyolultsága szempontjából: minél nagyobb a terület, annál bonyolultabb minta kialakulása várható. Példa erre a gepárd vagy a leopárd, amelyek bundájának összetett foltjai farkuk végén sávokká egyszerűsödnek. Érdekes módon ugyanezt a jelenséget figyelhetjük meg a futballmezek tervezésénél is: néhány kivételtől eltekintve a mezek ujjának mintázata egyszerűbb magának a meznek a mintájánál. Kivételek a természetben is akadnak, például a gyűrűsfarkú maki. Maini professzor előadásában példákat mutatott arra, hogy a kémiai reakciók során keletkező minták a természetben is mind megjelennek különböző állatok bundáján.
 Turing-mintázatok és megfelelőik különböző állatfajokon
Turing-mintázatok és megfelelőik különböző állatfajokon
Előadása második felében Maini professzor gerjeszthető rendszerekről beszélt, azaz olyan rendszerekről, amelyekben bizonyos hullámok terjedhetnek, és amelyekben nem terjedhet újabb hullám bizonyos idő eltelte előtt. Ennek kapcsán a professzor olyan mintázatokról beszélt, amelyek időben változnak. Példaként a Beluszov–Zsabotyinszkij-reakciót említette (olyan reakció, melynek során valamilyen szerves szubsztrátumot oxidálnak savas bromáttal átmenetifém-ionok jelenlétében). A reakciót leíró egyenletben néhány változó nagyon gyorsan változik, mások nagyon lassan, emiatt a rendszer hirtelen átugorhat egyik állapotból egy másikba. Az élővilágban hasonló jelenséget figyelhetünk meg a sejtes nyálkapenész nevű amőbánál (Dictyostelium discoideum). Ezek az amőbák tápanyaghiány esetén egy vegyületet bocsátanak ki, amelynek hatására összeállnak és egyebek mellett spórává differenciálódnak, ami segít a túlélésükben. Ebben a rendszerben olyan folyamatok játszódnak le (jelátvitel és sejtkommunikáció, kémiai mozgási ingerek, sejtdifferenciálódás), amelyek magasabb rendű élőlényekre jellemzőek, ezért egy kiváló fejlődésbiológiai modellrendszert szolgáltatnak. Ez is egy gerjeszthető rendszer, és megfigyelték, hogy az amőbák csoportosulása során spirális hullámmintázatok alakulnak ki. Egy másik nyálkagombafaj, a Physarum polycephalum képes arra, hogy az egysejtűekből álló telep a lehető legrövidebb úton érje el a táplálékot. Az organizmusok számára kellemetlen ízű koffeint a gombák kikerülték, más típusú alakzatot kialakítva. Később a telepek rájöttek, hogy érdemes átküzdeni magukat az akadályokon található irritáló anyagokon. Mindezeket a mintázatokat parciális differenciálegyenletes modellekkel is vissza lehet adni. Alan Hodgkin és Andrew Huxley 1952-ben a tintahal axonjában generált akciós potenciál leírására alkottak modellt, feltételezve, hogy az idegmembrán inger hatására bekövetkező feszültségváltozása az akciós potenciál ionáramokkal írható le, és hogy az ioncsatornák nyitását és csukását a kémiai reakciók kinetikájának mintájára lehet leírni. A két tudós a tintahal axonjából kiváltott akciós potenciál alakját egyenleteik segítségével számítógépes szimulációkkal reprodukálta, munkájukért 1963-ban kaptak Nobel-díjat. Denis Noble és Peter Hunter a szív működését modellezték. A szív elektromos impulzus hatására húzódik össze, ami hullámként terjed tovább az egész szíven. Ha a szív egy része elhal pl. oxigénhiány miatt, az megzavarja a hullámokat, és spirálok keletkeznek, ami fibrillációhoz, szívrohamhoz vezet.
A példák sokaságával Maini professzor megmutatta, hogy a matematikai modellezés segítségével számos biológiai és kémiai folyamatot érthetünk meg sokszor meglehetősen kontraintuitív módon, és ezzel új kutatási irányokat is inspirálhatunk. A matematikai megközelítésben rejlő absztrakció teszi lehetővé, hogy az egyik alkalmazásban használt ötleteket átvigyük egy másik területre.
Köszönetnyilvánítás
A cikk az Emberi Erőforrások Minisztériuma ÚNKP-19-4 Kódszámú Új Nemzeti Kiválóság Programjának támogatásával készült.
Dénes Attila
tudományos munkatárs, SZTE Bolyai Intézet









