Jelen ismeretterjesztő dolgozat egy háromrészes cikksorozat első része. A cikksorozat legfőbb célja egy konkrét mérnöki problémán keresztül illusztrálni az elméleti- és alkalmazott tudományok közötti összefonódást. Igyekeztünk olyan témát választani, amelynek tárgyalásához elegendő mindössze néhány egyszerű matematikai és fizikai fogalmat ismerni. Az is szempont volt, hogy láthatóak legyenek az absztrakt megközelítés előnyei, és hogy az egyszerűség ellenére legyenek nem magától értetődő alkalmazások és általánosítások.
Elsőként összefoglaljuk, hogy milyen témákat fogunk érinteni.
I. Vázlatosan ismertetjük a (csak ohmos ellenállásokat tartalmazó) ![]() -port hálózat fogalmát, és megmutatjuk, hogy hogyan modellezhető lineáris algebrai módszerekkel a hálózat rövidre zárása. Bevezetjük a cikksorozat legfontosabb fogalmát, a négyzetes mátrixok lineáris alterekre vonatkozó zárlatát (shorted matrix, vagy shorted operator [1,2]). Noha a technikai részleteket el fogjuk hagyni, nyilvánvaló lesz, hogy a legegyszerűbb jelenségek modellezéséhez is komoly nehézségeket kell áthidalni. Azt is látni fogjuk, hogy a modellezés során elvégzett munka megtérül, ugyanis a kapott képlet segítségével a probléma megoldása néhány mérésre, és algoritmikusan elvégezhető számolásokra egyszerűsödik.
-port hálózat fogalmát, és megmutatjuk, hogy hogyan modellezhető lineáris algebrai módszerekkel a hálózat rövidre zárása. Bevezetjük a cikksorozat legfontosabb fogalmát, a négyzetes mátrixok lineáris alterekre vonatkozó zárlatát (shorted matrix, vagy shorted operator [1,2]). Noha a technikai részleteket el fogjuk hagyni, nyilvánvaló lesz, hogy a legegyszerűbb jelenségek modellezéséhez is komoly nehézségeket kell áthidalni. Azt is látni fogjuk, hogy a modellezés során elvégzett munka megtérül, ugyanis a kapott képlet segítségével a probléma megoldása néhány mérésre, és algoritmikusan elvégezhető számolásokra egyszerűsödik.
II. Szintén egy alkalmazott probléma által motiválva bevezetjük a párhuzamos összegzés fogalmát, és az első részben megismert fogalmak végtelen dimenziós általánosításait. Megmutatjuk továbbá, hogy ez az általánosítás nem önmagáért való. Nevezetesen, ez az úgynevezett operátor képterekre vonatkozó általánosított zárlat kulcsszerepet játszik egy tisztán elméleti (ráadásul sokáig megoldatlan) probléma tisztázásában [3].
III. Természetes módon adódik a kérdés, hogy ha ezek az áramkörök elméletéből származó fogalmak ilyen hasznosak a lineáris leképezések elméletében, akkor nem lehetne-e ezekkel analóg fegyvereket bevetni a matematika más területein. A sorozat záró részében megadjuk a klasszikus mértékelmélet egyik alapvető fontosságú tételének egy olyan bizonyítását, amely (még ha ez eslő ránézésre nem is látszik), épp a lineáris altérre vett zárlat extremális tulajdonságaival operál [4].
1. Áramkörök modellezése
Bonyolult áramkörök modellezésénél gyakori módszer, hogy az áramkör belső működését egy fekete doboznak tekintik, és csak a ki- és bemeneteken megjelenő áramerősséget és feszültséget vizsgálják. Egy ki- és bemenet párt portnak neveznek, ha a rajta ki- és befolyó áram azonos nagyságú és ellentétes irányú. Megjegyezzük, hogy a port feltétel egy 1-port hálózaton épp az első Kirchoff-törvénynek felel meg. Az olyan rendszereket, melyeken ![]() ilyen pár található,
ilyen pár található, ![]() -port hálózatoknak nevezik [6]. Az egyszerűség kedvéért a fizikai jelenségeket
-port hálózatoknak nevezik [6]. Az egyszerűség kedvéért a fizikai jelenségeket ![]() -port hálózatokon fogjuk szemléltetni.
-port hálózatokon fogjuk szemléltetni.

1. ábra. Egy ![]() -port hálózat sematikus rajza.
-port hálózat sematikus rajza.
Az áramerősség és feszültség kapcsolatát ![]() -port hálózatokban a jól ismer Ohm-törvény (
-port hálózatokban a jól ismer Ohm-törvény ( ![]() ) adja meg, ahol
) adja meg, ahol ![]() az ellenállás nagysága. Egy kizárólag ohmos ellenállásokat tartalmazó
az ellenállás nagysága. Egy kizárólag ohmos ellenállásokat tartalmazó ![]() -port hálózatban az áramerősséget egy
-port hálózatban az áramerősséget egy ![]() , a feszültséget egy
, a feszültséget egy ![]()
![]() -dimenziós vektorral jelöljük, az impedancia pedig egy
-dimenziós vektorral jelöljük, az impedancia pedig egy ![]() -es pozitív szemidefinit valós
-es pozitív szemidefinit valós ![]() mátrixszal adható meg. Mivel
mátrixszal adható meg. Mivel ![]() -nek teljesítenie kell az
-nek teljesítenie kell az ![]() egyenlőséget, ezért az
egyenlőséget, ezért az
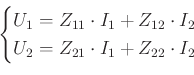
egyenletrendszerből az ![]() és
és ![]() paraméterek nullára állításával azt kapjuk, hogy
paraméterek nullára állításával azt kapjuk, hogy
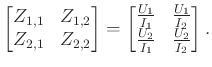
Látjuk tehát, hogy a lineáris algebra fogalmai hasznunkra válnak elektromos hálózatok modellezésénél. Nézzük meg, hogy egy egyszerű fizikai jelenség, nevezetesen az elektromos hálózat rövidre zárása (shorted circuit) miként realizálódik a modellben. Legyen tehát ![]() egy kizárólag ohmos ellenállásokat tartalmazó
egy kizárólag ohmos ellenállásokat tartalmazó ![]() -port hálózat. Ennek impedancia-mátrixáról megmutatható, hogy valós elemű és pozitív szemidefinit. Tegyük fel, hogy
-port hálózat. Ennek impedancia-mátrixáról megmutatható, hogy valós elemű és pozitív szemidefinit. Tegyük fel, hogy ![]() darab portot rövidre zárunk. Természetes módon adódik a kérdés, hogy mi az így kapott hálózat
darab portot rövidre zárunk. Természetes módon adódik a kérdés, hogy mi az így kapott hálózat ![]() impedancia-mátrixa, és hogy látható-e konkrét algebrai kapcsolat
impedancia-mátrixa, és hogy látható-e konkrét algebrai kapcsolat ![]() és
és ![]() között. Ahogy az lenni szokott, most sem a kérdés, de még csak nem is a válasz, hanem a felhasznált módszer lesz az érdekes.
között. Ahogy az lenni szokott, most sem a kérdés, de még csak nem is a válasz, hanem a felhasznált módszer lesz az érdekes.
A portok megfelelő sorbarendezésével elérhető, hogy a ![]() mátrix felírásában a jobb alsó
mátrix felírásában a jobb alsó ![]() -es blokk feleljen meg a rövidre zárandó résznek. Ekkor világos, hogy az impedancia csökken,
-es blokk feleljen meg a rövidre zárandó résznek. Ekkor világos, hogy az impedancia csökken, ![]() -ben pedig csak a bal felső
-ben pedig csak a bal felső ![]() -es blokkban lehetnek nem nulla elemek, ugyanis feszültség csak a rövidre nem zárt portokon maradhat fenn.
-es blokkban lehetnek nem nulla elemek, ugyanis feszültség csak a rövidre nem zárt portokon maradhat fenn.
2. Négyzetes mátrixok lineáris alterekre vonatkozó zárlata
A továbbiakban legyen ![]() egy
egy ![]() -dimenziós valós vagy komplex Hilbert-tér a szokásos skalárszorzattal, és jelölje
-dimenziós valós vagy komplex Hilbert-tér a szokásos skalárszorzattal, és jelölje ![]() a pozitív szemidefinit mátrixok kúpját. Ahhoz, hogy legyen értelme annak mondatnak, hogy „az impedancia csökken”, be kell vezetnünk egy alkalmas részbenrendezést
a pozitív szemidefinit mátrixok kúpját. Ahhoz, hogy legyen értelme annak mondatnak, hogy „az impedancia csökken”, be kell vezetnünk egy alkalmas részbenrendezést ![]() -n. Egy
-n. Egy ![]() mátrixra azt mondjuk, hogy
mátrixra azt mondjuk, hogy ![]() , ha
, ha ![]() , azaz ha
, azaz ha
Legyen ![]() egy
egy ![]() -dimenziós lineáris altér
-dimenziós lineáris altér ![]() -ban. Bizonyos értelemben ez az
-ban. Bizonyos értelemben ez az ![]() altér reprezentálja majd a rövidre nem zárt
altér reprezentálja majd a rövidre nem zárt ![]() darab portot. Azt a jelenséget, hogy a rövidre zárt hálózatban feszültség csak ezeken a portokon lehet, úgy írhatjuk le, hogy
darab portot. Azt a jelenséget, hogy a rövidre zárt hálózatban feszültség csak ezeken a portokon lehet, úgy írhatjuk le, hogy
Tehát ahhoz, hogy megkapjuk a rövidre zárt hálózat impedancia-mátrixát, be kell azonosítsuk az
halmaznak a ![]() részbenrendezésre nézve legnagyobb elemét. Azaz azt a
részbenrendezésre nézve legnagyobb elemét. Azaz azt a ![]() elemet, amelyre teljesül, hogy
elemet, amelyre teljesül, hogy
Az azonban, hogy ilyen mátrix létezik, egyáltalán nem magától értetődő. Hogy a ![]() részbenrendezés sajátosságait előrevetítsük, megjegyezzük, hogy még az olyan egyszerű szerkezetű halmazok is tartogatnak meglepetéseket, mint két mátrix-intervallum metszete. A cikksorozat második részében meg fogjuk mutatni, hogy a
részbenrendezés sajátosságait előrevetítsük, megjegyezzük, hogy még az olyan egyszerű szerkezetű halmazok is tartogatnak meglepetéseket, mint két mátrix-intervallum metszete. A cikksorozat második részében meg fogjuk mutatni, hogy a
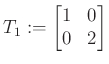 és
és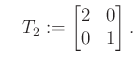
választással az
halmaznak nincs legnagyobb eleme (noha az egységmátrix egy nagyon szimpatikus jelölt). Ezt úgy is mondhatjuk, hogy ![]() -nek és
-nek és ![]() -nek nincs legnagyobb közös alsó korlátja.
-nek nincs legnagyobb közös alsó korlátja.
Visszatérve az eredeti kérdéshez: az tehát egy bizonyítandó állítás, hogy az ![]() halmaznak létezik legnagyobb eleme. Magát a bizonyítást (lásd [2,5]) itt nem közöljük, de értelmes és korrekt a következő definíció.
halmaznak létezik legnagyobb eleme. Magát a bizonyítást (lásd [2,5]) itt nem közöljük, de értelmes és korrekt a következő definíció.
Definíció: Legyen ![]() egy tetszőleges mátrix, és legyen
egy tetszőleges mátrix, és legyen ![]() lineáris altér. Ekkor az
lineáris altér. Ekkor az ![]() halmaz legnagyobb elemét (amely létezik és egyértelmű) a
halmaz legnagyobb elemét (amely létezik és egyértelmű) a ![]() mátrix
mátrix ![]() -zárlatának nevezzük és
-zárlatának nevezzük és ![]() -sel jelöljük. Igaz továbbá, hogy
-sel jelöljük. Igaz továbbá, hogy
Külön megemlítjük azt az esetet, amikor a vizsgált ![]() mátrix invertálható. Ekkor ugyanis a (meglehetősen technikai) bizonyítás nem pusztán a létezést garantálja, hanem formulát ad
mátrix invertálható. Ekkor ugyanis a (meglehetősen technikai) bizonyítás nem pusztán a létezést garantálja, hanem formulát ad ![]()
![]() -zárlatának mátrixára. Tekintsük a
-zárlatának mátrixára. Tekintsük a ![]() mátrix
mátrix ![]() -hez tartozó blokkfelbontását. Legyenek tehát
-hez tartozó blokkfelbontását. Legyenek tehát ![]() ,
, ![]() ,
, ![]() ,
, ![]() a megfelelő blokkok. Ekkor
a megfelelő blokkok. Ekkor
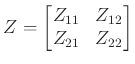 és
és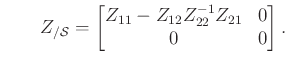
3. Mit nyertünk?
Most ismét az invertálható esetre szorítkozunk. A fenti leírás azt mutatja (és ez a valódi mondanivaló), hogy ha ismerjük a hálózat impedancia-mátrixát, és tudjuk, hogy mely portokat zártuk rövidre, akkor meg tudjuk mondani a rövidre zárt hálózat impedancia-mátrixát anélkül, hogy bármit is tudnánk a hálózat belső tulajdonságairól.
Sőt, ennél többet is állíthatunk: a ![]() mátrix ismeretében a válasz algoritmikusan, és nagyon gyorsan megadható. Valóban, a
mátrix ismeretében a válasz algoritmikusan, és nagyon gyorsan megadható. Valóban, a ![]() mátrixokat
mátrixokat ![]() -ből erőfeszítés nélkül megkaphatjuk, a
-ből erőfeszítés nélkül megkaphatjuk, a ![]() mátrix inverzének kiszámítására van algoritmus. Ezek után pedig csak két szorzást és egy kivonást kell elvégeznünk.
mátrix inverzének kiszámítására van algoritmus. Ezek után pedig csak két szorzást és egy kivonást kell elvégeznünk.
Szemléltetésként nézzük meg egy végtelenül egyszerű példán, hogy hogyan végezhetőek el a számítások a fenti matematikai módszerek elkerülésével.
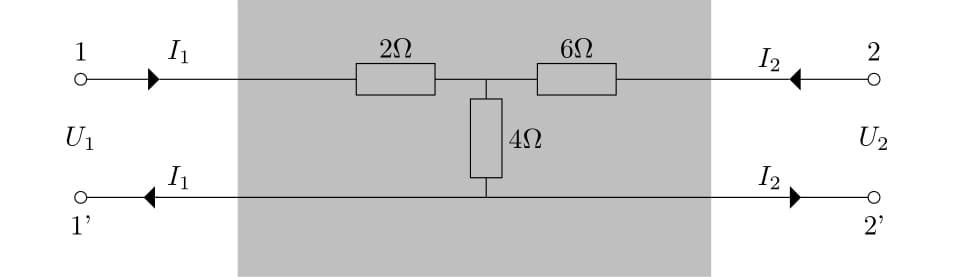
2. ábra. Egy egyszerű ![]() -port hálózat
-port hálózat
Először is határozzuk meg a 2. ábrán látható hálózat impedancia-mátrixát. Kirchhoff első és második törvényét felhasználva könnyen adódik az
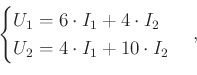
egyenletrendszer, melyből az együtthatók kiolvasásával kapjuk, hogy a vizsgált ![]() -port hálózat impedancia-mátrixa
-port hálózat impedancia-mátrixa
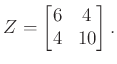
Zárjuk most rövidre a hálózat második portját.
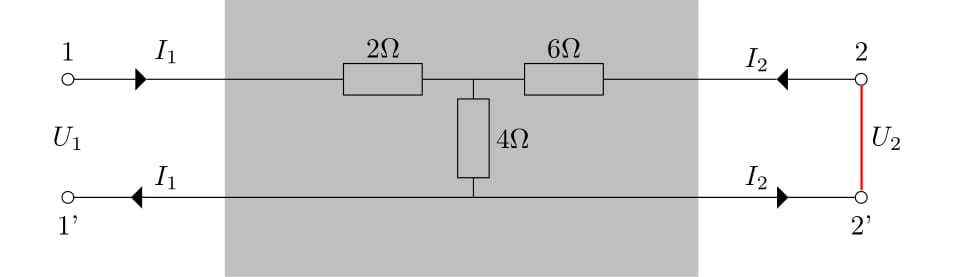
3. ábra. A fenti ![]() -port hálózat rövidre zárása
-port hálózat rövidre zárása
A 3. ábrára ránézve azt látjuk, hogy a ![]() -os és
-os és ![]() -os ellenállások párhuzamos kapcsolásba kerültek, így ezek egy
-os ellenállások párhuzamos kapcsolásba kerültek, így ezek egy ![]() eredő ellenállású ellenállással helyettesíthetőek. Kihasználva, hogy ez az új
eredő ellenállású ellenállással helyettesíthetőek. Kihasználva, hogy ez az új ![]() -os ellenállás egy
-os ellenállás egy ![]() -os ellenállással került soros kapcsolásba, megkapjuk, hogy az új eredő
-os ellenállással került soros kapcsolásba, megkapjuk, hogy az új eredő ![]() , azaz
, azaz
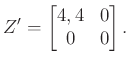
Vegyük észre, hogy a számolás elvégzéséhez rengeteg információra volt szükségünk. Látni kellett, hogy a rövidre zárással hogyan módosul az ellenállások egymáshoz viszonyított helyzete, melyik mivel cserélhető le, és így tovább. Ezek külön-külön mind egyszerű lépések, de egy bonyolult (sok ellenállást tartalmazó) hálózat esetén okozhatnak némi kellemetlenséget.
A fenti okoskodásnál jóval egyszerűbb ránézni a ![]() mátrixra, és a
mátrixra, és a
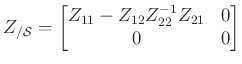
képletbe behelyettesítve azonnal megkapni, hogy a rövidre zárt hálózat impedanciája
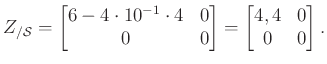
A cikkben vázlatosan bevezetett mátrix operáció (azaz az altérre vonatkozó zárlat) tisztán elméleti hasznával a következő részben fogunk foglalkozni.
A cikksorozat az Emberi Erőforrások Minisztériuma ÚNKP-18-4-BGE-3 kódszámú „Új Nemzeti Kiválóság Programjának” támogatásával készül.
Irodalomjegyzék
- [1] Anderson, W. N., Shorted operators, SIAM Journal on Applied Mathematics Vol. 20, No. 3 (1971), 520–525.
- [2] Anderson, W. N., Trapp, G. E., Shorted operators II., SIAM Journal on Applied Mathematics Vol. 28, No. 1 (1975), 60–71.
- [3] Ando T. Problem of Infimum in the Positive Cone, In: Rassias T.M., Srivastava H.M. (eds) Analytic and Geometric Inequalities and Applications. Mathematics and Its Applications, vol 478. Springer, Dordrecht (1999).
- [4] Titkos, T., A simple proof of the Lebesgue decomposition theorem, American Mathematical Monthly, 122 (2015) 793–794.
- [5] Ujszászi, Z. A Lebesgue-felbontás egy operátorelméleti megközelítése, BSc Szakdolgozat (2018).
- [6] Yang, W.Y., Seung C. L., Circuit Systems with MATLAB and PSpice, John Wiley & Sons (2007).
mesterszakos egyetemi hallgató
MTA Rényi Alfréd Matematikai Kutatóintézet
és Budapesti Gazdasági Egyetem









