Azt mondják, hogy a matematikusok között igen sok zenészt találni. Ez nem meglepő, hiszen mind a zene keltésében, mind magában a rezgő közeg fizikai viselkedésében, sőt, a zene lejegyzésében is rengeteg matematikailag könnyen leírható tulajdonságot fedezhetünk fel. Az, hogy a szép, s logikus rend mellé gyönyörködtető hangzás is párosul, magához vonzza a szépség iránt amúgy is igen érzékeny matematikusokat. Szoktuk is mondogatni a matematikában, hogy ha egy bizonyítás szép, akkor az nagy valószínűséggel jó is.
Monochord — arany aránypár
Mint minden előadást, ezt is úgy illik kezdeni, hogy „már a görögök is…” Nem véletlen ez, hiszen az emberiség történetével egyidős lehet a — sokszor alig-alig ismert — zenei művészet. Valóban kevéssé ismert a régi idők zenéje, gondoljunk csak arra, hogy az egyik legszebb hangú hangszerünket a torkunkban hordozzuk… Sajnos, a régi emberek hangszereiről is kevés feljegyzés maradt fenn, s már a pár száz évvel ezelőtti hangszerek rekonstrukciója is nehéz feladat. A zene lejegyzése is elég későn alakult ki a történelem folyamán, nem is beszélve arról, hogy mit tekintett fontosnak lekottázni a korabeli zenész, s mi volt az, amit nem írt le, hiszen közismert tény volt.
De ha már a görögök, akkor természetesen — matematika tanárok lévén — rögtön Pitagorasz jut eszünkbe. Pitagorasz nevével kapcsolatban pedig háromszögekre gondolunk, s a velük kapcsolatos tételre. De gondolunk-e arra a Pitagoraszra, aki kitartóan érdeklődött a tiszta művészetek iránt? Gondolunk-e Pitagoraszra, mint filozófusra? Gondolunk-e Pitagoraszra, aki az élet számos területén kereste a rendet, ahogy ő nevezte, a szümphoniát?

https://upload.wikimedia.org/wikipedia/commons/0/0b/MIM_String_Instruments.jpg
Közismert a történet, amelyet Pitagorasz nevéhez fűznek. Nevezetesen egy kalapácsműhely mellett elhaladva a négy kalapács csengését konszonánsnak, azaz szépen együttszólónak hallotta, s e tulajdonságot a kalapácsok súlya közötti összefüggéssel azonosította. A kedves história szép képet fest a nagy matematikusról, de kevéssé valószínű. Annyi viszont bizonyos, hogy igen behatóan tanulmányozta a monochord rezgéseit (lásd a fenti képen). Ilyen egyhúrú hangszer csupán az iskolában fellelhető, az is csak demonstráció céljából. Azonban ne keseredjünk el, szinte mindenki talál a környezetében egy gitárt, ami céljainknak tökéletesen megfelel. Ennek teste kiválóan rezonál, erősíti a húr alig hallható hangját. Takarjuk le a nem szükséges húrokat, hogy kizárjuk azok zavaró hatását. Ezen a hangszeren már könnyedén kísérletezhetünk, hála a bundoknak, a fogólapon található rézlapoknak, melyek segítségével bárki tisztán lefoghatja a hangokat mindenféle zenei előképzettség nélkül.

Játsszunk a gitárunkkal! Egyetlen húrt — pl. a legalsó, a legvastagabb E-húrt — megpendítve más és más magasságú hangot kapunk, ha a húrt egy-egy bundnál lefogjuk. Pitagorasz hasonló kísérleteket végzett a monochordjával: a húrt 12 egyenlő hosszúságú részre osztotta fel, így könnyedén vette a húr felét, harmadát, … (Szerencsére a 12-nek sok osztója van! ☺) Így ha most a felénél fogjuk le a húrt, akkor megpengetéskor az alaphang feletti oktávot, ha a 2/3-ad részénél, akkor a kvintet, s ha a 3/4-ed részénél, akkor a kvartot hallhatjuk. (Sok gitárnál a bundok közötti jel segítségünkre van az oktáv, s a kvart lefogásánál.) A kísérletet a többi húron elvégezve ugyanezeket a hangközöket figyelhetjük meg.
A kis egész számok arányaként felírt húrarányok meglepő módon éppen azok a hangközök, melyeknél a két hangot (alap és oktáv, alap és kvart, illetve alap és kvint) a leginkább szépen együttcsengőnek érzünk. (Ennek okára még később visszatérünk.) Amit a zenében szépnek találunk, az a matematikában is igen szép arányokkal, az arany aránypárral írható fel. Lássuk, mi is ez!
![]()
Az ábrán láthatjuk, hogy a 12 egység hosszúságú húrt a kilencediknél lefogva az alaphang kvartját kapjuk meg, míg ha a 8 egység hosszúságú húrral tesszük ugyanezt, akkor a 6 egységnél kell lefognunk a húrt, hogy a rövidebb húr kvartját hallhassuk. Ezt matematikailag a ![]() arány igazolja.
arány igazolja.
Emellett még szintén érdekes, hogy a 9 (kvart) és a 8 (kvint) a 12 (alaphang) és a 6 (az alap oktávja) számtani, illetve harmonikus közepe:
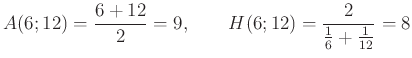
Tehát az „arany aránypárt” ezekkel felírva:
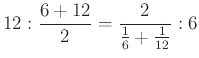
Pitagorasz a kozmosz szóval nevezte el a világ e szép harmóniáját. A szép rend számára mindenhol megjelent. Így például a kocka és duálisa, az oktaéder között figyelt meg szép rendet:
| kocka | oktaéder |
| 6 lap | 6 csúcs |
| 8 csúcs | 8 lap |
| 12 él | 12 él |
A szépre való törekvésünket minden művészetben megfigyelhetjük. A képeken, szobrokon, épületeken, de a drámák, zeneművek időbeli felépítésében is lépten-nyomon felfedezhetjük a kis egész számokkal felírható arányokat, vagy akár az aranymetszést. Ennek oka az ember, az ember és környezete, a világ harmonikus felépítésében keresendő. Nem véletlen, hogy Orfeusz muzsikájával a holtakra és élőkre is egyaránt hatással van, rezonálnak zenéjére.
Hangközök — összegzés a zenében
Térjünk vissza az egyhúrú hangszerünkhöz. Mi is történik a húrral, ha megpendítjük?

A húr két végén rögzítve van, így szemmel látható, hogy a kifeszített drót a pendítés irányában, illetve ellentétesen kitér, egy orsószerű mintázatot hoz létre. Ez egy fél hullámhossz, hiszen a teljes szinusz görbe fele jelenik meg előttünk.
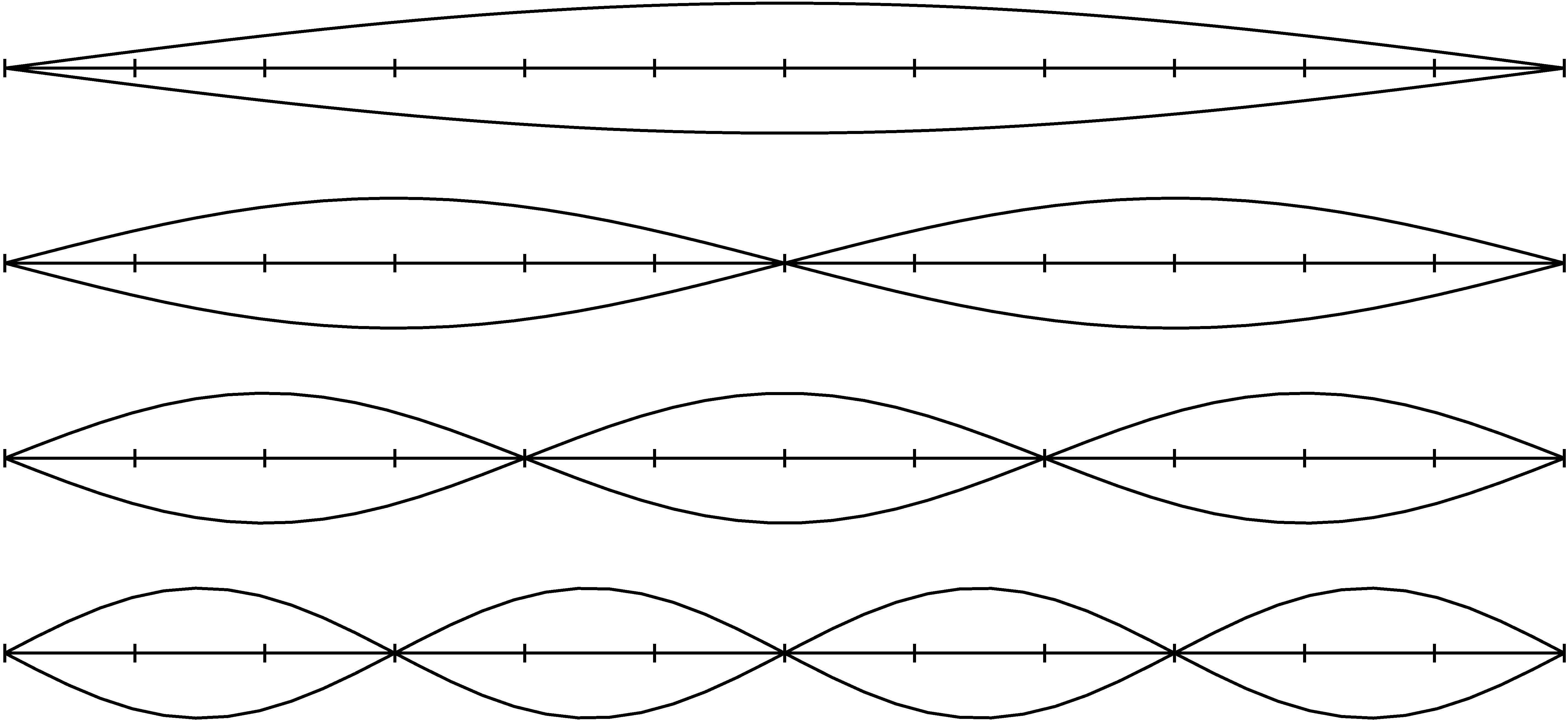
Ez azt jelenti számunkra, hogy a húron létrejövő rezgés hullámhossza éppen a húr hosszának a kétszerese lesz. Hasonlóképpen a húr hosszát rövidítve (lefogva egy-egy bundnál a húrt) a hullámhossz arányosan változik.
A hullámhossz és a frekvencia fordítottan arányos. (Lásd később, a szorzatuk éppen a hangsebességet adja meg az adott közegben.)
Vegyük most alaphangnak az egyvonalas ![]() hangot. A következő kottaképen az alaphangot és az oktávját láthatjuk egy-egy másik hanggal két további hangközre bontva. Így az első esetben az oktávot egy kvint és egy kvart, míg a második esetben egy kvart és egy kvint összegére bontottuk. Világos, hogy a két összeg ugyanazt az oktávot adja, vagyis az összeadás kommutatív tulajdonsága jelenik meg:
hangot. A következő kottaképen az alaphangot és az oktávját láthatjuk egy-egy másik hanggal két további hangközre bontva. Így az első esetben az oktávot egy kvint és egy kvart, míg a második esetben egy kvart és egy kvint összegére bontottuk. Világos, hogy a két összeg ugyanazt az oktávot adja, vagyis az összeadás kommutatív tulajdonsága jelenik meg:

De hogy néz ki matematikailag ez az összegzés? Írjuk fel a húrhosszak arányát! (Oktáv: ![]() , kvart:
, kvart: ![]() , kvint:
, kvint: ![]() .) Látható, hogy most az összeadás jel helyett a szorzás jelét kell használnunk, hogy az
.) Látható, hogy most az összeadás jel helyett a szorzás jelét kell használnunk, hogy az ![]() arányt megkapjuk:
arányt megkapjuk:
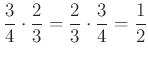
Ha a hangok összegzését a húrhosszak arányának szorzásával kell felírnunk, akkor ez egy matematikus számára azt jelenti, hogy a kotta a húrok arányainak logaritmusát (sőt ld. később, a frekvenciák logaritmusát) ábrázolja:
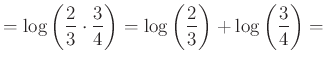 kvint és kvart kottaképe
kvint és kvart kottaképe
Ha már az előbb felfedeztük, hogy tetszőleges húron végezhetjük a megfigyeléseinket, miért ne folytatnánk azzal a húrral, amellyel a játékot elkezdtük? Arra gondolok, hogy ha a húron a 3/4-ed részt lefogva előállíthattam az E-húr kvintjét, azaz a H hangot, akkor megismételhetnénk a lefogást most a megrövidített húron, előállítva a H hang kvintjét. Ehhez nem kell mást tenni, mint a korábbi, a „megmaradt” 2/3-ad hosszúságú húr 2/3-ád kell venni. Így máris a H hang kvintjét hallhatjuk, a Fisz hangot.
Matematikailag ez azt jelenti, hogy az eredeti húr 2/3-ad részének 2/3-ad részét vettük, azaz a ![]() -ed részét vettük a húrnak. Zeneileg pedig azt mondhatjuk, hogy a kvintre ráépítettünk egy újabb kvintet. Matematikus gondolkodásunk máris érzi, hogy a zenei összegzés, a két kvint összeadása a hangok frekvenciájának szorzását fogja jelenteni…
-ed részét vettük a húrnak. Zeneileg pedig azt mondhatjuk, hogy a kvintre ráépítettünk egy újabb kvintet. Matematikus gondolkodásunk máris érzi, hogy a zenei összegzés, a két kvint összeadása a hangok frekvenciájának szorzását fogja jelenteni…
Konszonancia
Ismét visszatérve az egyhúrú hangszerünkhöz, vegyük fel gyorsított videóval a húr rezgéseit. Amint a felvételt lassítva visszanézzük, észrevehetjük, hogy a korábban szabad szemmel is jól látható orsószerű alakzatra további furcsa, de egyben mégis szabályos rezgések rakódnak rá. Ez azt jelenti, hogy a húr rezgésében további, rövidebb hullámhosszú rezgések találhatók.

Ezt kísérletileg könnyen ellenőrizhetjük, csupán annyi a dolgunk, hogy az alaphang rezgését megszüntessük. Ezt úgy tesszük meg, hogy a megpendítés után a húr közepét óvatosan megérintjük, mellyel a közepén megszüntetjük a rezgését. Ekkor a további rezgéseket hallhatjuk, közülük is a legerősebb az oktáv hangja lesz. (Ha a húr középen nem rezeg, akkor két orsószerű alakzat jön létre rajta, vagyis egy teljes szinuszhullám, melynek hullámhossza a húr hossza.)
Ha a kísérletet most úgy folytatjuk, hogy a húr 2/3-ánál is megszüntetjük a rezgést, akkor az alaphang kvintjét hallhatjuk — igaz, egy oktávval feljebb. Tovább kísérletezve (ehhez már nagy ügyesség kell a gitáron) a további részhangokat is kinyerhetjük. Ezek a hangok a következő sorrendben jönnek elő:

Az egyes hangok alá írt számok nem csupán a sorrendet jelentik, hanem azt is, hogy az alaphang frekvenciájának (![]() ) hányszorosa jött létre:
) hányszorosa jött létre: ![]() . Ez jól érthető a korábbi ábránkon, hiszen a kísérleteink során éppen egy-egy újabb orsószerű alakzat „fér rá” a húrra.
. Ez jól érthető a korábbi ábránkon, hiszen a kísérleteink során éppen egy-egy újabb orsószerű alakzat „fér rá” a húrra.
Ezt hívjuk felhangskálának. (Érdekességként érdemes megemlíteni, hogy a hangok különböző hangszínét éppen ezen felhangok különböző erőssége határozza meg. A fuvola hangjában pl. a felhangok egyenletesen csökkenő erősségűek, míg a klarinét felhangjai a csökkenő erősség mellett kissé hiányosak: minden második felhang hiányzik.)
Korábbi tapasztalatainkból érdemes rögzítenünk, hogy az oktávok frekvenciái mindig az előzők kétszeresei (![]() ), míg a kvinteket egy 3/2-es szorzással állíthatjuk elő (
), míg a kvinteket egy 3/2-es szorzással állíthatjuk elő (![]() ).
).
Mitől szól szépen két hang együtt? Közelítsük meg máshonnan a kérdést. Szép-e együtt a 440 Hz-es és a 441 Hz-es hang? (A 440 Hz-es hang azt jelentik, hogy a húr, a levegő részecskéi, a dobhártyánk, … éppen 440-et rezeg egy másodperc alatt. A 440 Hz-es hangot nevezzük a zenei A hangnak, erre hangolnak a zenekarok.)
Érdemes letölteni egy hanggenerátort a telefonunkra. Ilyen igen sokféle található. Például a Frequency Sound Generator segítségével egyszerre több frekvenciájú hangot is hallhatunk.
A két képen a nagyon magas rezgésszám nem lenne jól látható, helyette a 11 Hz-es, a 12 Hz-es, a jobboldali ábrán pedig a két előző összegével kiegészített rezgések láthatók.

A hangfelvételekre kattintva a 440 Hz-es, a 441 Hz-es, valamint e kettő összegét (a két hang együttes hangját) hallgathatjuk meg.
440 Hz-es hang:
441 Hz-es hang:
a két hang összege:
Ha külön-külön hallgatjuk e két hangot, nem halljuk a különbséget. Ellenben együtt érdekes hanghatást figyelhetünk meg: a hallott hang egy változó intenzitású hang lesz. Ennek okát igen egyszerűen magyarázhatjuk matematikailag.
A két rezgés:
A kettőt összeadva a következő függvényt kapjuk:
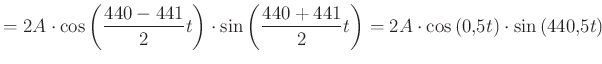
A kapott eredményen látszik, hogy a rezgés továbbra is szinuszos (a kettő átlagával, egy 440,5 Hz-cel rezgő hangot hallunk), melynek amplitúdója lassan — 0,5 Hz-cel — változik. (A 440,5 Hz-hez képest a 0,5 Hz igen kicsi frekvenciájú.) Ezt halljuk lebegésszerűnek.
Maga a hallható hangzás nem túl szép, de kiválóan használható hangoláshoz: amikor a két hang frekvenciája igen közel van egymáshoz, a lebegés lassan megszűnik:
![$\displaystyle =\lim_{\varepsilon\to 0}\left[2A\cdot\cos\left(\frac{\varepsilon}...
...\sin\left(\left(440+\frac{\varepsilon}{2}\right)t\right)\right]=2A\sin(440 t)
$](/images/stories/latex/aa8b2b6eec7cd1909260641d07d49192_szekelypeterzenematematika/img35.png)
Ugyanígy nem túl szép két hang együtt, ha felhangjai között van „súrlódás”, vagyis van olyan két felhang, melynek frekvenciái igen közel vannak egymáshoz.
A legszebb két hang, mely igen kellemesen együtt szól, a tiszta prím, vagyis az, mikor két ugyanolyan frekvenciájú hang szól. (Azonos a két hang.) Ekkor természetes, hogy minden felhang megegyezik. Ha a két hang egy oktávnyira van egymástól, akkor egész sok egyezés található a felhangok között, s alig van néhány hang, mely „súrlódik”. A kvarttal és a kvinttel már sokkal több baj van. Mint az alábbi táblázatból látszik, jóval kevesebb az egyezés. (A ', '', ''', stb. jelzések azt jelentik, hogy hány vonalas hangról van szó, vagyis, hogy az alaphang felett hány oktávval van a hang magasabban.)
| C | C' | G' | C'' | E'' | G'' | B'' | C''' | D''' | E''' | Fisz''' | G'''' |
| C' | C'' | G'' | C''' | E''' | G'''' | ||||||
| G' | G'' | D''' | D'''' | ||||||||
A kvintnél az G alaphangra épülő sorban igen kevés egyezés van (G', G'', D''', G''''):
| G | G' | D'' | G'' | H'' | D''' | F''' | G''' | A''' | H''' | E'''' | G'''' |
|---|
A kvartnál az F alaphangra épülő sorban még kevesebb egyezés van (C'', C''', G'''):
| F | F' | C'' | F'' | A'' | C''' | Esz''' | F''' | G''' | A''' | H''' | F'''' |
|---|
A zenében a terc igen későn került a játszott hangközök közé. Ezt a hangközt igen sokáig disszonánsnak tartották.
A következő hangmintákat meghallgatva egészen archaikusnak tűnik az oktáv, illetve régies, gregoriánszerű a kvint párhuzamban hallható Tavaszi szél vizet áraszt kezdetű dal. (A szekund távolságra lévő két szólamot bántó hallgatni.)
tiszta prím:
oktáv:
kvint:
szekund:
A pitagoraszi hangsor
Ha csupán az oktávot tekintjük szépen konszonáns hangzatnak, akkor a többi hangközt nem fogjuk használni.
A kvint is igen szépen együttcsengő hangköz. Használjuk fel a skálánk felépítéséhez. Mielőtt matematikázunk, ismételjük át egy kicsit a fizikai ismereteinket!
Tanultuk, hogy a levegőben kb. 340 m/s a hang sebessége, ami nem más, mint az egyetlen hanghullám hullámhossza osztva a hozzá szükséges idővel, a periódusidővel, vagy másként: a hullámhosz és a frekvencia szorzata.
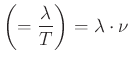
Az adott közegben ez a sebesség állandó, tehát a hullámhossz (![]() ) és a frekvencia (
) és a frekvencia (![]() ) fordított arányban áll egymással. Az előzőeket egy táblázatban összefoglalva láthatjuk az összefüggéseket a zenei kifejezések (oktáv, kvart, kvint) között. Alaphangnak a gitár legalsó, legvastagabb húrját, az E húrt választottuk:
) fordított arányban áll egymással. Az előzőeket egy táblázatban összefoglalva láthatjuk az összefüggéseket a zenei kifejezések (oktáv, kvart, kvint) között. Alaphangnak a gitár legalsó, legvastagabb húrját, az E húrt választottuk:
| alaphang (E) | |
|
| kvart (A) | |
|
| kvint (H) | |
|
| oktáv (e) | |
|
A következőkben válasszuk alaphangnak az egyvonalas c hangot. Mint az előzőekből látható volt, ennek a kvintjét úgy kaphatjuk meg, hogy a c hang frekvenciáját 3/2-del szorozzuk. Így nyerjük az egyvonalas g hangot. Ennek a kvintjét ismét egy 3/2-des szorzással állíthatjuk elő. Ez lesz a kétvonalas d hang. Az eljárást folytatva az a, e, h, fisz, cisz, gisz, disz, aisz, fiszisz(=f) és c hangokat kapjuk. Látható, hogy az eljárásunk segítségével, kvintugrásokkal előállítottuk az európai zenében előforduló összes hangot. Szokás ezt a lépéssorozatot a kvintkörön ábrázolni:
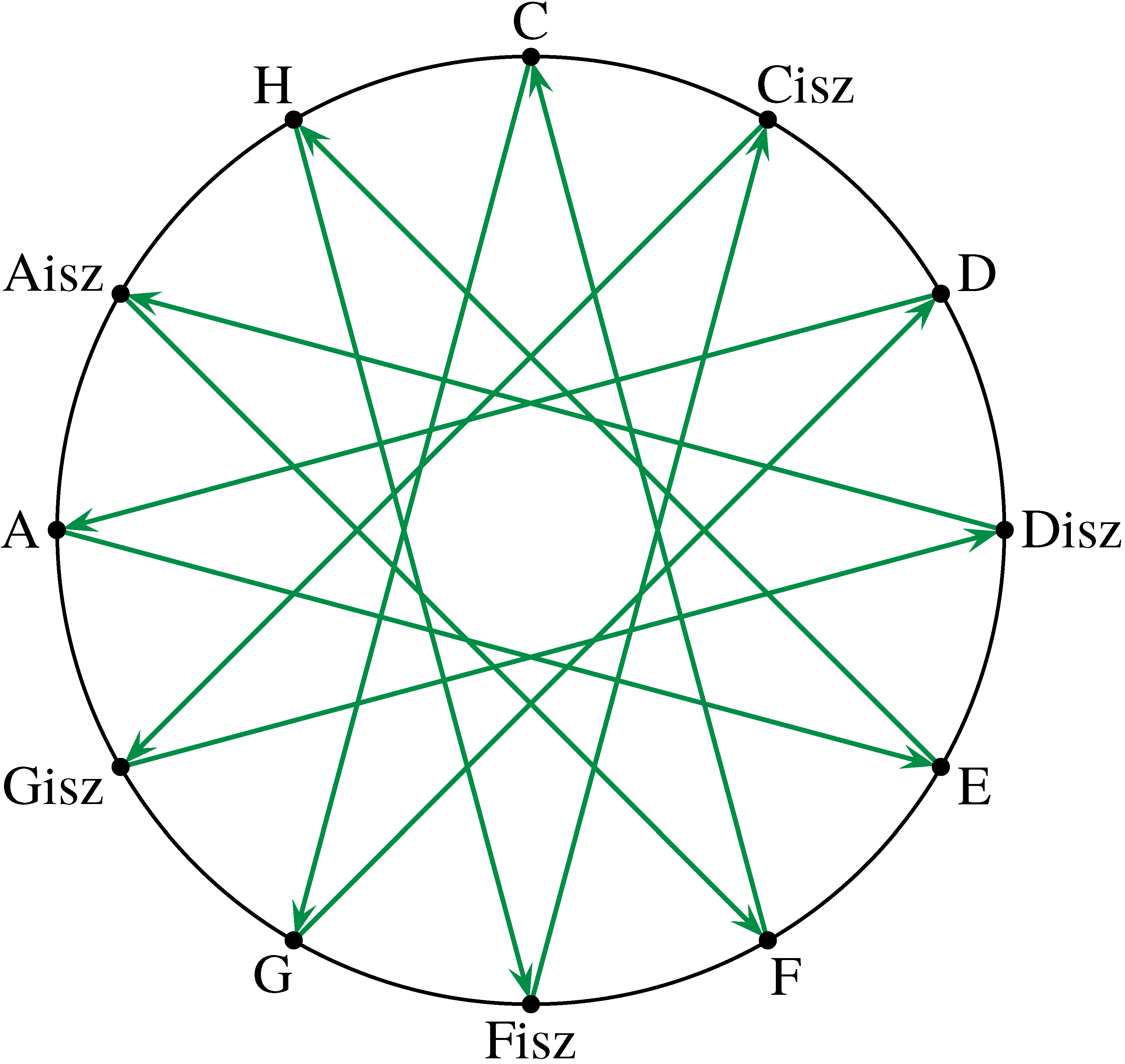
A nyilak iránya a frekvenciák ![]() -del való szorzását jelzi. A tizenkettedik ugrás után az alaphang egy oktávjához jutottunk vissza.
-del való szorzását jelzi. A tizenkettedik ugrás után az alaphang egy oktávjához jutottunk vissza.
Valóban megkaptuk az alaphang valamelyik oktávját? A frekvenciákat 3/2-del szorozgatva előállítható az oktáv (melyet az alaphang kettővel való szorzásával nyerhetünk)?
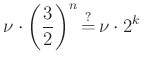
Az egyenlőség igaz lehet? Természetesen nem, hiszen ![]() . A hiba viszont olyan elenyésző, hogy — néhány kiváló zenésztől eltekintve — mindenki élvezni fogja így is a muzsikát. Részletezve az állítást:
. A hiba viszont olyan elenyésző, hogy — néhány kiváló zenésztől eltekintve — mindenki élvezni fogja így is a muzsikát. Részletezve az állítást:
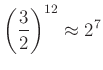
A kvintugrásokkal felépített skálával nyerhetjük a pitagoraszi hangsort. Ehhez csupán annyit kell tennünk, hogy néhány esetben az egy oktávval lejjebbi hangot választjuk a kapott hang helyett. (Ez a frekvencia 2-vel való osztását jelenti.)

Az egyes hangok közötti hangközök így a következőképpen alakulnak:
| c | d | e | f | g | a | h | c | |||||||
| |
|
|
|
|
|
|||||||||
| |
|
|
|
|
|
|
Az így nyert pitagoraszi hangsor valóban szép hangközöket eredményez egy adott alaphangról kiindulva. A későbbi zenében (barokk kortól kezdve) felmerült az igény, hogy a zenemű közben más hangnembe, egy más alaphangról indított skálába is szeretnének áttérni a zenészek. Ebben a skálában viszont a legtisztább hangközeink (kvart, kvint) nem lesznek már olyan szép konszonánsak, mint az alapskálában. (Pl. a c-ről indított skálában a „végén” csalnunk kellett, hogy az oktávhoz visszatérjünk. Ha példának okául a H hangot vesszük alapul, akkor a csalás miatt most már a kvint sem lesz tiszta konszonáns…)
Bach idejében ezt az eltérést egy Zarlino nevű zenetudós megelőző kutatásai alapján úgy oldották meg, hogy az alaphang és oktávja közötti részt 12 teljesen egyforma hangközre bontották fel. A kérdés az volt, hogy mi lehet az a szám, mellyel 12-szer megszorozva az alaphang frekvenciáját, az oktávhoz jutunk. Matematikailag felírva
egyenlet megoldását jelenti. ![]() lesz ez a szám, mellyel két egymás melletti hangközt (kis szekundot) előállíthatjuk. A kvint most nem lesz olyan szép, konszonáns hangköz, hiszen
lesz ez a szám, mellyel két egymás melletti hangközt (kis szekundot) előállíthatjuk. A kvint most nem lesz olyan szép, konszonáns hangköz, hiszen
![$\displaystyle \frac{3}{2}\cdot\nu_0=\left(\sqrt[12]{2}\right)^7\approx 1{,}4983\cdot\nu_0,
$](/images/stories/latex/aa8b2b6eec7cd1909260641d07d49192_szekelypeterzenematematika/img83.png)
de az eltérés elhanyagolható talán. A hangszereinket ma így hangolják (temperált skála), s a parányi eltérések kiküszöbölésére a zenész hivatott.
Kezdő tanár koromban is szívesen forgattam Sain Marci bácsi matematikatörténeti könyvét, a Nincs királyi utat. Szeretettel ajánlom tanítványaimnak ma is, ezt a ma már csak könyvtárban fellelhető remekművet. A cikk e művel való „összecsengése” tehát nem a véletlen műve, kedvenc irodalmam volt ez a könyv.
A rövid írás figyelemfelkeltő szeretne csupán lenni, minden teljességre, részletre való törekvés nélkül. Az előadás szűkre szabott ideje (30 perc) is hasonlóképpen ízelítőt kívánt adni a zeneelméletről, s a benne rejlő matematikáról, fizikáról. Igyekeztem, hogy e hatalmas anyagban minden korosztály számára legyen a matematikaórákhoz kapcsolódó érdekes kitekintés. Kérem, hogy mindenki kedvére folytassa a kísérletezést, s a zene matematikai felfedezéseit.
Székely Péter
Székely Péter a budapesti Eötvös József Gimnázium matematika, fizika és informatika szakos tanára. Gyermekkora óta zenél, elvégezte a budapesti Bartók Béla Zeneművészeti Konzervatóriumot, s ma is örömmel muzsikál zenésztársaival (Triola Fúvósegyüttes). Zeneszeretetét igyekszik gyermekeinek, tanítványainak is átadni.









