Információk

 Aktuális szám: 4. szám 2017. június 

Programozás — Wolfram nyelv

Programozás — Wolfram nyelv

Arra a kérdésre, hogy a matematikában vagy a programozásban kell-e pontosabbnak lennünk, valószínűleg többen mondanák azt, hogy az elsőben, mint a másodikban, és talán ez is a gyakoribb eset. Most mégis mutatunk két (egymáshoz közeli) példát az ellenkezőjére.

Ha adott az $ A$ és a $ B$ nem üres halmaz, és az $ f\colon A\to B$ függvény, továbbá a függvény értelmezési tartományának $ C\subset A$ részhalmaza, akkor szükségünk lehet a $ C$ halmaz elemeinek képeiből álló halmazra. A matematikus tehát bevezeti az $ f(C):=\{f(x)\vert x\in C\}$ jelölést, mit sem törődve azzal a ténnyel, hogy az $ f$ függvény $ A$ elemein, és nem $ A$ részhalmazain volt értelmezve! Ha itt pontosabbak akarnánk lenni (bár valóban nem okoz igazán gondot ez a pongyolaság), akkor az $ f$ függvény által generált, $ A$részhalmazait $ B$ részhalmazaiba képező függvényről van szó, amit a halmaz (angolul set) szó kezdőbetűjével tehetünk nyomatékosabbá, például így: $ Sf(C):=\left\{f(x)\mid x\in C\right\}$ ( $ C\subset A$). Kézenfekvő, hogy a programnyelvek esetén világosan meg kell különböztetni az $ f$ és az $ Sf$ függvényt, de valahogyan a kapcsolatukat sem árt számon tartani. A Wolfram nyelv (leánykori nevén Mathematica, hogy ne csak Wolfram Alpha és Wolfram Science létezzék reklámhordozóként) bevezette a Map ,,kétváltozós'' függvényt (ha tetszik: operátort) erre a célra. Ha tehát adott például a $ C:=\{a,b,c\}$ halmaz és az $ f$ függvény, akkor a $ C$ halmaz képe ennél a függvénynél, vagyis az $ \{f[a],f[b],f[c]\}$ halmaz így számolható: $ \textbf{Map}[f,\{a,b,c\}]$. (Megjegyzendő, hogy egy idő után a Maple fejlesztői is kénytelenek voltak bevezetni ezt a függvényt.)

Nézzünk egy másik példát! Ha most $ f$ olyan függvény, amely a sík pontjainak koordinátáihoz rendel valamit, akkor értékét az épeszű így számolja: $ f(x,y)$. A furmányos viszont természetesen így: 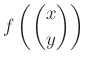$ f\left(\dbinom{x}{y}\right)$, hiszen függvényünk kétdimenziós vektorokhoz rendel valamit, nem számpárokhoz! (Aki teheti, gondoljon még arra is, hogy TeX-ben hány karakter kell, hogy ehhez a szép alakhoz eljussunk!) Amikor erről mégis szó esik, például analízisben, akkor eleinte az az ember érzése, hogy folyamatosan azonosítunk mindent önmagával, pedig tényleg két különböző fogalomról van szó. A Wolfram-nyelv erre a problémára a következő megoldást kínálja: Ha adott az $ \{x,y\}$ vektor, és szeretnénk, ha komponensei az $ f$ kétváltozós függvény argumentumaiként szerepeljenek, akkor ezt kell írnunk: $ \textbf{Apply}[f,\{x,y\}]$, az eredmény pedig $ f[x,y]$ leend.

A figyelmes Olvasó észrevehette, hogy egyszer halmazt, egyszer meg vektort mondtam. Ha a Wolfram nyelv értelmében pontos akartam volna lenni, akkor mindkét esetben listát kellett volna mondanom, ugyanis ez az ott használt alapvető adatszerkezet.

A programnyelv alaposabb tanulmányozása közben kiderül, hogy a fent bevezetett két operátor elképesztően hasznos eszköznek bizonyul. Lásd erről programozóknak vagy a közönséges halandóknak szóló bevezetőket.

TJ

Megjegyzések:

A Wolfram nyelv történetéről 2016. szeptemberi számunkban Lóczi Lajos írt: http://ematlap.hu/index.php/gazda-g-sag/340-a-wolfram-programozasi-nyelv-rovid-tortenete-3 .

A TeX programozási nyelv keletkezéséről mostani számunkban olvashatnak Kovács Zoltán cikkében.

Fényképünkön Wolfram 2008-ban, forrása: https://hu.wikipedia.org/wiki/Stephen_Wolfram (Stephen Wolfram's PR team/Stephen Faust. Received via email from Stephen Wolfram's staff. Publicity photo of Stephen Wolfram).

 

 

 

 

 

2017-05-28