A Boy-felület a projektív síknak a háromdimenziós térbe való immerziója (tehát csak transzverzális önátmetszésekkel rendelkező beképezése), amelyet Werner Boy talált 1901-ben [1] (miután Hilbert megbízta azzal, hogy lássa be, a projektív síknak nem létezik immerziója a háromdimenziós térbe). Az Interneten rengeteg csodálatos kép található erről az immerzióról, most belülről fogjuk ezt felépíteni, hogy jól láthatóak legyenek a Boy-felület tulajdonságai.
Először is, az immerziónak szükségszerűen lesz egy háromszoros pontja, ahol három sík találkozik oly módon, ahogy a koordinátasíkok találkoznak ![]() origójában. Valóban, egy
origójában. Valóban, egy ![]() immertált felület háromszoros pontjainak száma modulo 2 megegyezik
immertált felület háromszoros pontjainak száma modulo 2 megegyezik ![]() első Stiefel–Whitney osztályának
első Stiefel–Whitney osztályának ![]() -ben lévő négyzetével (ami a projektív sík esetében 1).
-ben lévő négyzetével (ami a projektív sík esetében 1).
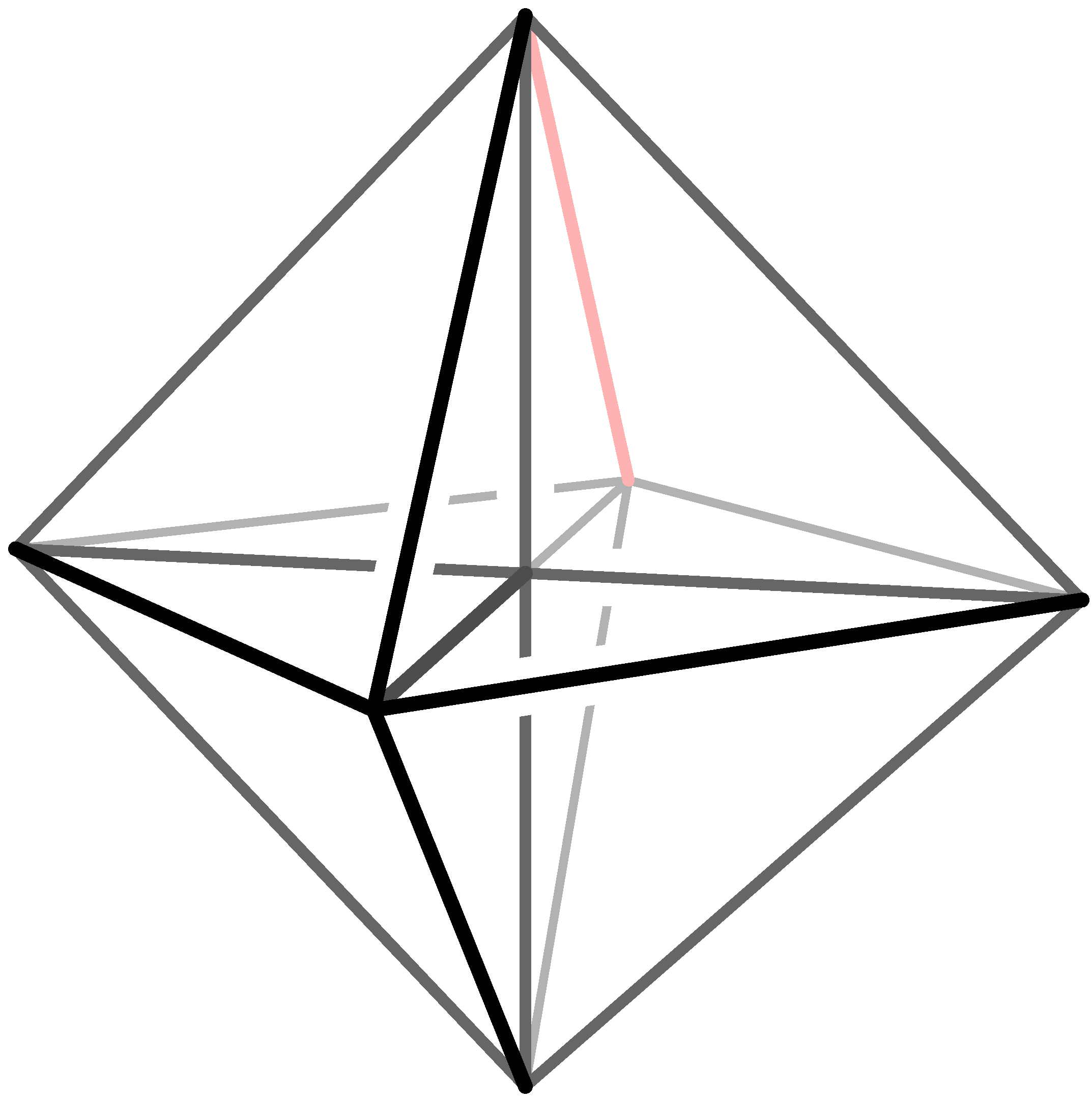
1. ábra
Vegyük az ![]() síkban azt a négyzetet, amelynek négy csúcsa a
síkban azt a négyzetet, amelynek négy csúcsa a ![]() és
és ![]() pontokban van, és vegyük a hasonló négyzeteket az
pontokban van, és vegyük a hasonló négyzeteket az ![]() és
és ![]() síkokban, ahogy azt az 1. ábra is mutatja. A kapott poliéder élváza a Park City Matematikai Intézet (PCMI) logója; ez a logó inspriálta 2006 júliusi előadásomat erről a témáról Park City-ben. A most bemutatandó konstrukció nem tőlem származik, de nem tudok arról, hogy ez valaha megjelent volna. Nekem Bob Edwards mondta el a PCMI intézetben, és neki is a logóról jutott eszébe.
síkokban, ahogy azt az 1. ábra is mutatja. A kapott poliéder élváza a Park City Matematikai Intézet (PCMI) logója; ez a logó inspriálta 2006 júliusi előadásomat erről a témáról Park City-ben. A most bemutatandó konstrukció nem tőlem származik, de nem tudok arról, hogy ez valaha megjelent volna. Nekem Bob Edwards mondta el a PCMI intézetben, és neki is a logóról jutott eszébe.

2. ábra
Adjunk tehát az 1. ábrához négy 2-szimplexet (vagyis háromszöglapot) a „szemközti” háromszögek mentén; ezek közül kettőt, egy sötét lilát és egy bíbort a 2. ábrán szemléltetünk. Itt „szemközti” azt jelenti, hogy a négy 2-szimplex közül semelyik kettőnek nincs közös éle. A kapott ![]() poliéder egy kétdimenziós sokaság (azaz felület), mivel minden él egy négyzeten és egy háromszögön fekszik; és a hat szimmetrikus csúcsnál egy nyolcas-alak (egy kör síkba immertált képe egyetlen duplaponttal) feletti kúpot kapunk, ami egy absztrakt kétdimenziós körlap. A négyzetek és háromszögek együtt az
poliéder egy kétdimenziós sokaság (azaz felület), mivel minden él egy négyzeten és egy háromszögön fekszik; és a hat szimmetrikus csúcsnál egy nyolcas-alak (egy kör síkba immertált képe egyetlen duplaponttal) feletti kúpot kapunk, ami egy absztrakt kétdimenziós körlap. A négyzetek és háromszögek együtt az ![]() projekív síkot adják, mivel a felület Euler-karakterisztikája
projekív síkot adják, mivel a felület Euler-karakterisztikája ![]() .
.
Vegyük észre, hogy a kocka minden csúcsát maximális módon levágva egy olyan testet kapunk, amelyet 8 háromszög (amelyek az eredeti kocka csúcsainak felelnek meg) és 6 négyzet határol (ezek a négyzetek az eredeti kocka lapjainak közepén voltak). Az átellenes pontokat azonosítva ![]() -t, illetve a fent megkonstruált
-t, illetve a fent megkonstruált ![]() poliédert kapjuk. Vegyük észre a kapott objektum szimmetriáit.
poliédert kapjuk. Vegyük észre a kapott objektum szimmetriáit.
![]() egyetlen problémája, hogy nem simán van beágyazva a háromdimenziós térbe. Az éleket még le tudjuk kerekíteni, a hat kúp-pontot azonban nem. Ezt megjavítandó, párosítsuk a 6 kúp-pontot a „szemközti” élekkel (az 1. ábrán egy ilyen élt pirosra színeztünk). Minden él felhasználható arra, hogy „kiküszöbölje” a 8-as alakú kúpokat az él végein, ahogy azt a 3–7. ábrák mutatják.
egyetlen problémája, hogy nem simán van beágyazva a háromdimenziós térbe. Az éleket még le tudjuk kerekíteni, a hat kúp-pontot azonban nem. Ezt megjavítandó, párosítsuk a 6 kúp-pontot a „szemközti” élekkel (az 1. ábrán egy ilyen élt pirosra színeztünk). Minden él felhasználható arra, hogy „kiküszöbölje” a 8-as alakú kúpokat az él végein, ahogy azt a 3–7. ábrák mutatják.
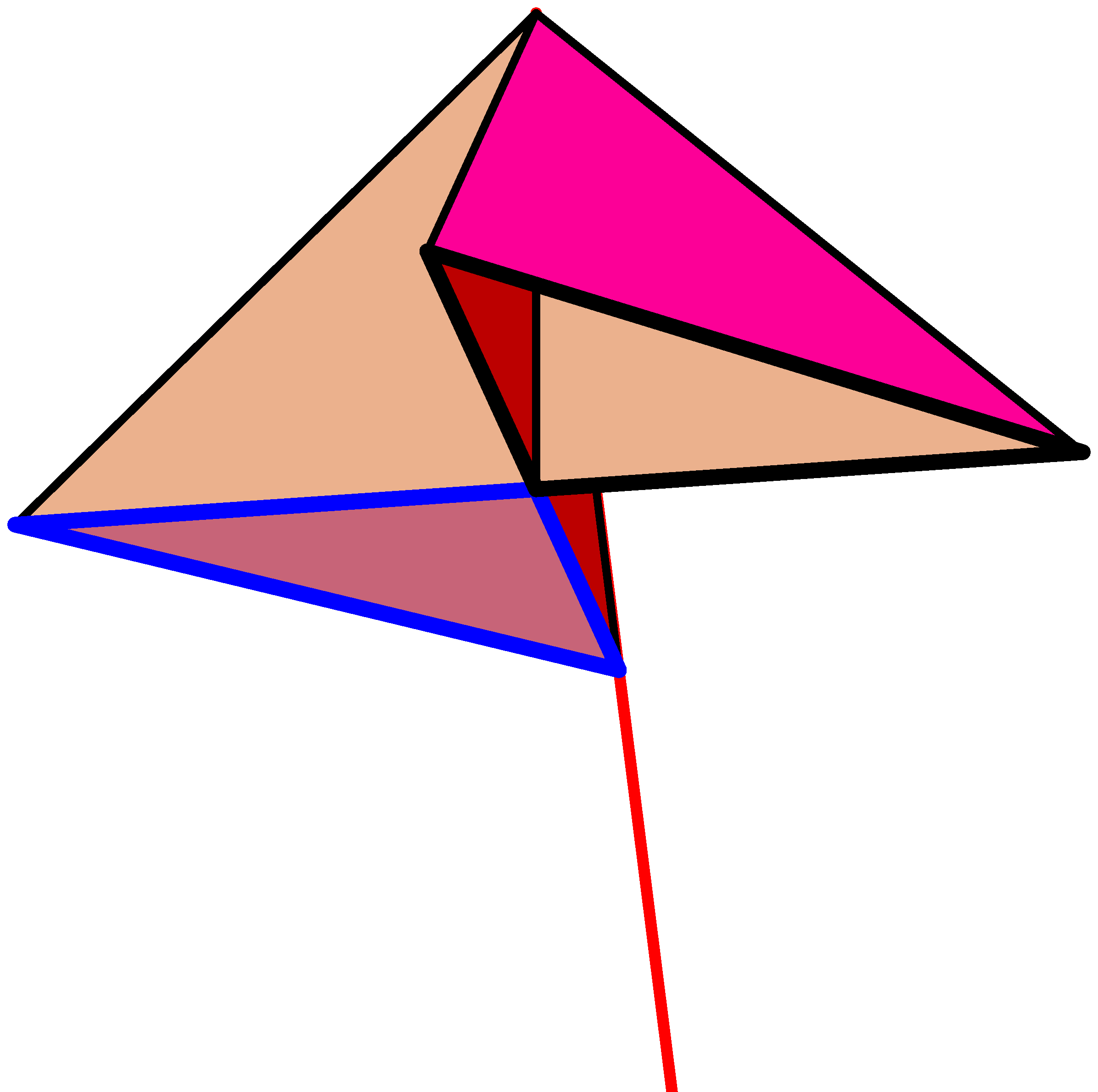
3. ábra
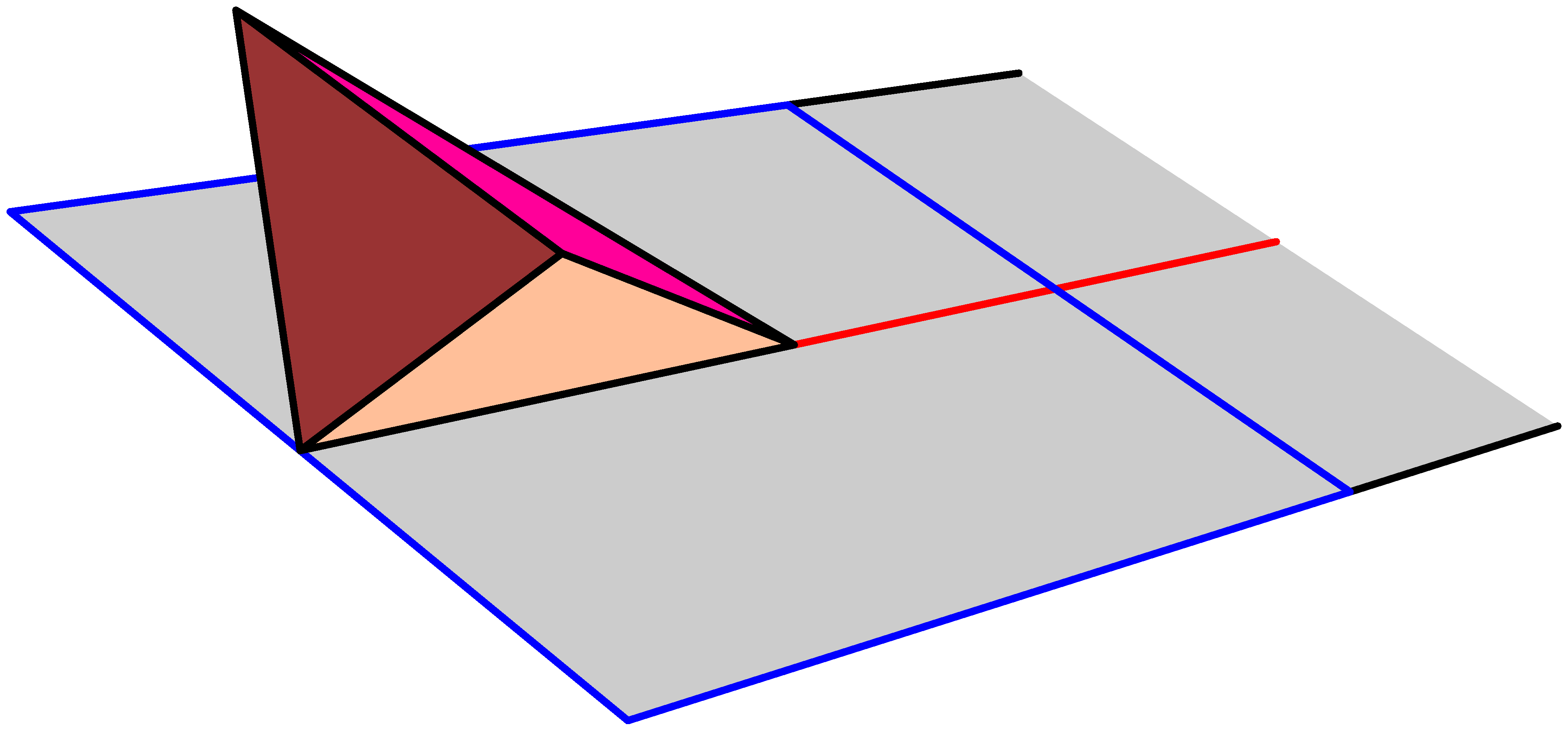
4. ábra
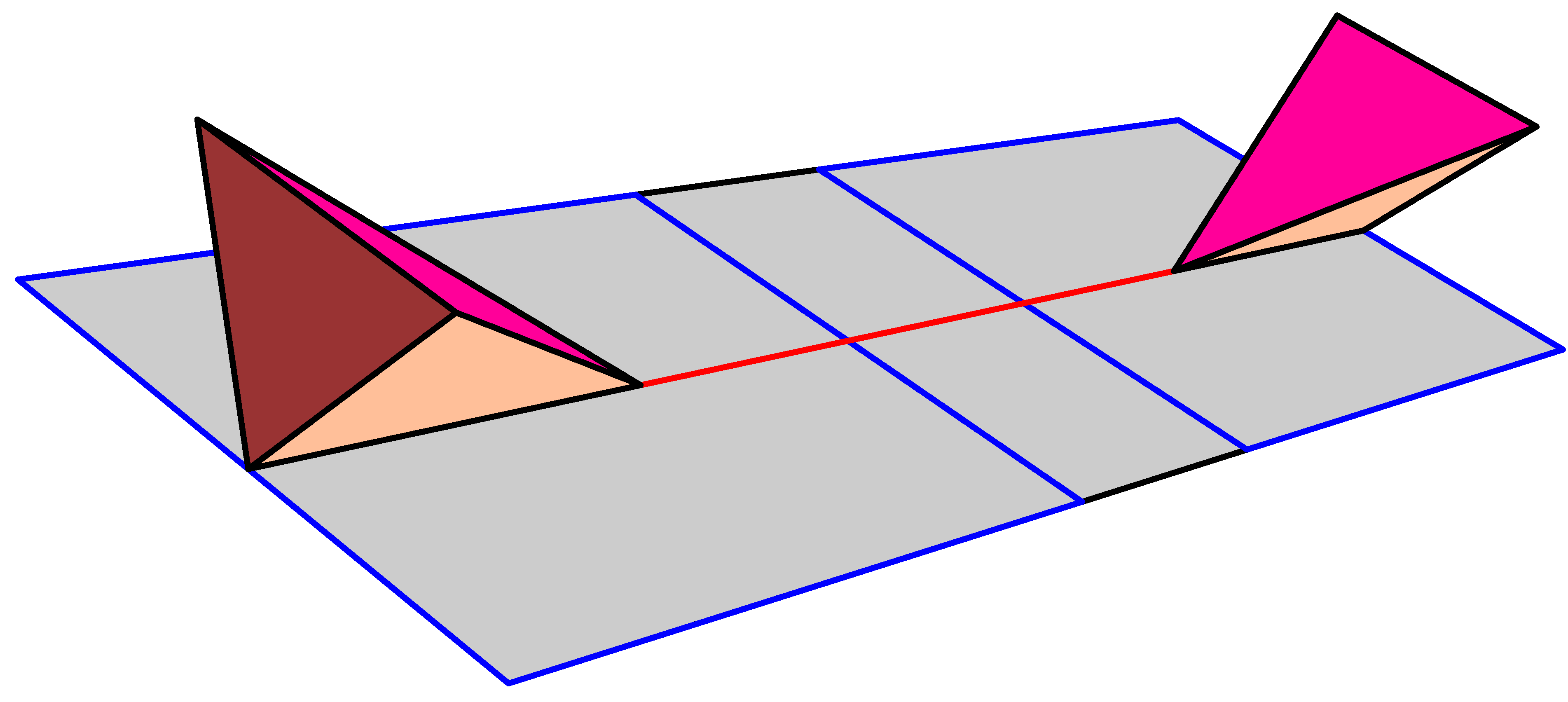
A felső csúcs egy környezetét mutatja meg a 3. ábra. Ez a környezet kilapítható, hogy úgy nézzen ki, mint ahogy azt a 4. ábra mutatja; ez továbbra is egy 8-as alak feletti kúp lesz. A piros él egy környezete úgy néz ki, ahogy azt az 5. ábra mutatja, mindkét végén egy kúp-ponttal. Ezt kilapítva a 6. ábra ![]() poliéderét kapjuk.
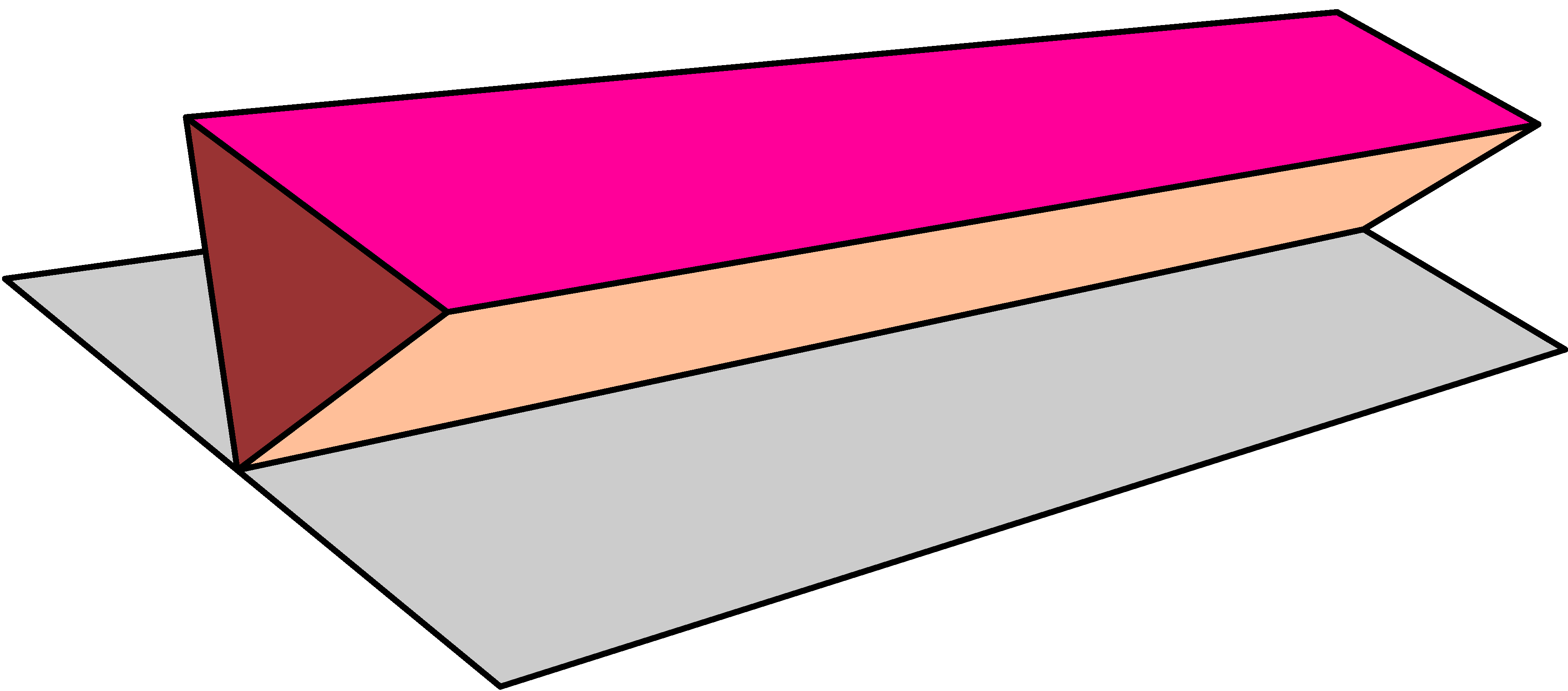
poliéderét kapjuk. ![]() valójában egy téglalap képe, amely immertált, kivéve a kúp-pontban. Ezt (a határt változatlanul hagyva) megváltoztatjuk, és a téglalap 7. ábrán mutatott immerziójára cseréljük, ahol a kúp-pontok eltűntek.
valójában egy téglalap képe, amely immertált, kivéve a kúp-pontban. Ezt (a határt változatlanul hagyva) megváltoztatjuk, és a téglalap 7. ábrán mutatott immerziójára cseréljük, ahol a kúp-pontok eltűntek.
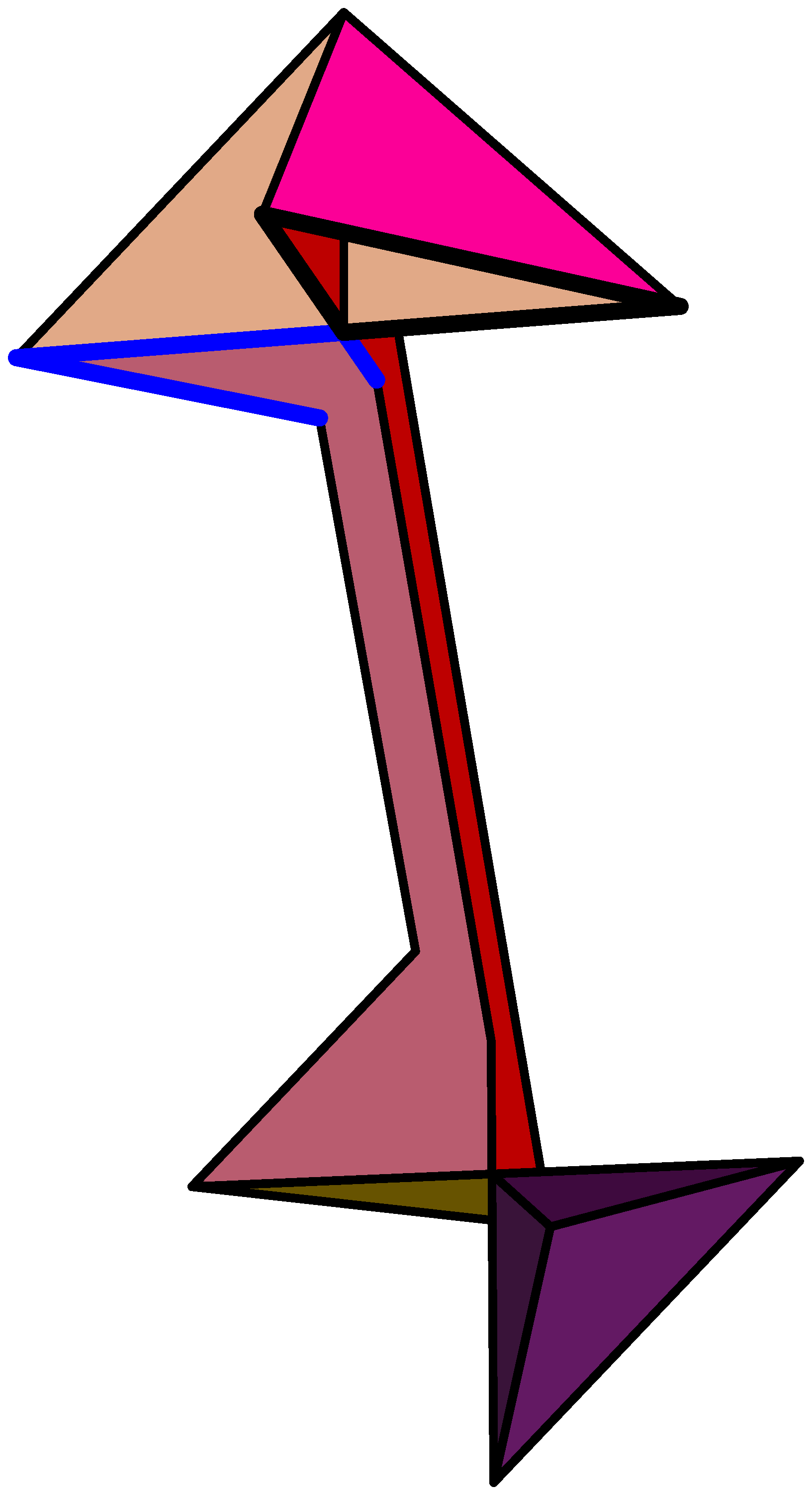
5. ábra
6. ábra
7. ábra
Amint ezt a műveletet mindhárom csúcspárra (a kúp-pontokra) végrehajtottuk, megkapjuk a Boy-felületet, a projektív sík egy immerzióját. Ez egy részenként lineáris (ún. PL) immerzió, de a csúcsok és élek könnyedén lekerekíthetőek, egy sima immerziót adva. Vegyük észre, hogy a duplapontok egy immertált körvonalat alkotnak, amely háromszor megy át a tripla-ponton. Ez az immertált kör ![]() eredeti koordinátatengelyeiből áll, egyesítve azzal a három éllel, amelyek segítségével a kúp-pontokat eltüntettük. E körvonal
eredeti koordinátatengelyeiből áll, egyesítve azzal a három éllel, amelyek segítségével a kúp-pontokat eltüntettük. E körvonal ![]() -beli környezete természetesen egy Möbiusz-szalag, amelynek komplementuma egy beágyazott körlap.
-beli környezete természetesen egy Möbiusz-szalag, amelynek komplementuma egy beágyazott körlap.
Ez a sima immerzió (vagy bármely másik) arra is használható, hogy illusztráljuk Smale gömbkifordítási tételét [2]. Ez a tétel azt mondja, hogy létezik a kétdimenziós gömbfelület ![]() -ba való immerzióinak egy olyan serege, amely kifordítja a gömböt; a létezési tételt eredetileg Smale látta be, és azóta több konstrukció jelent meg erről [2]. A projektív sík immertált képének normális 0-dimenziós gömbnyalábja (vagyis a normális
-ba való immerzióinak egy olyan serege, amely kifordítja a gömböt; a létezési tételt eredetileg Smale látta be, és azóta több konstrukció jelent meg erről [2]. A projektív sík immertált képének normális 0-dimenziós gömbnyalábja (vagyis a normális ![]() -nyaláb pereme) egy immertált kétdimenziós gömböt ad, és ez az immerzió kifordítható úgy, hogy az intervallumok végpontjait egymás felé mozgatjuk a
-nyaláb pereme) egy immertált kétdimenziós gömböt ad, és ez az immerzió kifordítható úgy, hogy az intervallumok végpontjait egymás felé mozgatjuk a ![]() intervallum mentén. Ez nem lesz generikus, mert félidőben épp a Boy-felületet kapjuk, míg egy generikus 1-paraméteres immerzióseregben nem találunk kétdimenziós többszöröspont-halmazt.
intervallum mentén. Ez nem lesz generikus, mert félidőben épp a Boy-felületet kapjuk, míg egy generikus 1-paraméteres immerzióseregben nem találunk kétdimenziós többszöröspont-halmazt.
Ahhoz hogy kifordítsuk a kétdimenziós beágyazott kerek gömböt, meg kell találnunk azt is, hogy hogyan mozgassuk ezt immerziókon keresztül az immertált projektív sík feletti 0-dimenziós gömbnyalábba, majd ebben a képben ezt a fentiek szerint átmozgatjuk önmagán, és az eredményt ismét (az első lépésben talált immerziósereg megfordításával) a kerek gömbbe visszük vissza.
Az első (és így a harmadik) lépésről pedig ismert, hogy megtehető. Egy immertált kétdimenziós gömb Gauss-leképezése a következő módon definiálható: rendeljük a gömb egy pontjához az ![]() -beli standard kétdimenziós gömb azon pontját, amely a választott pont kifelé mutató egység hosszú normálisa végpontjának felel meg. (Ehhez a gömb egy irányításának rögzítése szükséges, és a kifordítás alatt a kifelé mutató normális a befelé mutató normálisba fog mozogni.) A Boy-felület feletti normális 0-gömbnyaláb Gauss-leképezése egy 1-fokú leképezés, mivel a háromszöglapon levő normális az egyetlen abba az irányba mutató vektor. Smale-nek az ebben a dimenzióban lévő immerziókra vonatkozó tétele szerint ha két immerzió Gauss-leképezésének foka megegyezik, akkor a két immerzió összeköthető immerziók egy 1-paraméteres családjával. Emiatt tehát a gömb-kifordítás létezik, bár a Boy-felület csak azt mutatja meg, hogy az immertált 0-dimenziós nyaláb kifordítható.
-beli standard kétdimenziós gömb azon pontját, amely a választott pont kifelé mutató egység hosszú normálisa végpontjának felel meg. (Ehhez a gömb egy irányításának rögzítése szükséges, és a kifordítás alatt a kifelé mutató normális a befelé mutató normálisba fog mozogni.) A Boy-felület feletti normális 0-gömbnyaláb Gauss-leképezése egy 1-fokú leképezés, mivel a háromszöglapon levő normális az egyetlen abba az irányba mutató vektor. Smale-nek az ebben a dimenzióban lévő immerziókra vonatkozó tétele szerint ha két immerzió Gauss-leképezésének foka megegyezik, akkor a két immerzió összeköthető immerziók egy 1-paraméteres családjával. Emiatt tehát a gömb-kifordítás létezik, bár a Boy-felület csak azt mutatja meg, hogy az immertált 0-dimenziós nyaláb kifordítható.
Köszönetnyilvánítás: Köszönöm Bill Casselman-nak a kiváló képeket, és a Clay Mathematics Institute-nak a támogatásukat, amelyet a 2006-os Park City Mathematics Institute programja alatt nyújtottak.
Irodalomjegyzék
- [1] Werner Boy: Über die Curvatura Integra und die Topologie der Geschlossener Flächen, Dissertation, Göttingen, 1901; Math. Ann. 57 (1903), 151–184.
- [2] Anthony Phillips: Turning a surface inside out, Scientific American 214 (1966), no. 5, 112–120.
- [3] Stephen Smale: A classification of immersions of the two-sphere, Trans. Amer. Math. Soc. 90 (1958), 281–290.
Rob Kirby
- Rob Kirby a University of California, Berkeley professzora. A cikk ábráit Bill Casselman készítette, ő a University of British Columbia professzora és a Notices grafikai szerkesztője. A cikk eredetileg az American Mathematical Society Notices folyóiratának 2007 novemberi számában jelent meg a What is ...? rovatban. A fordítást Stipsicz András készítette.
Rob Kirby: What is Boy's Surface? Notices Amer. Math. Soc. Vol. 54 Num. 10. (2007 November) 1306-07 ©2007 American Mathematical Society. https://www.ams.org/notices/200710/tx071001306p.pdf









