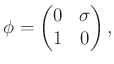Egy Higgs-nyaláb nem más, mint egy holomorf vektornyaláb és egy ún. Higgs-mező együttese. Ezek a fogalmak Nigel Hitchin Riemann-felületek feletti önduális egyenletekről írt tanulmányában, illetve Carlos Simpson doktori értekezésében és egy későbbi, nem-abeli Hodge-elméleti munkájában tűntek fel először. A mérceelmélet egyenleteiben fellépő hasonló objektumok elnevezése nyomán Hitchin bevezette a Higgs-mező fogalmát. Ebben az összefüggésben a Higgs-mező olyan fizikai részecskéket ír le, mint például a Higgs-bozon. Simpson javaslatára a „Higgs-nyaláb” elnevezés együtt utal egy nyalábra és egy Higgs-mezőre.
A Higgs-nyalábok gazdag struktúrát hordoznak, ami olyan területeken játszik szerepet mint a mérceelmélet, a Kähler- és hiperkähler-geometria, felületek fundamentális csoportjainak ábrázolásai, az integrálható rendszerek elmélete, a nem-abeli Hodge-elmélet, a mátrixszorzatok Deligne—Simpson-problémája és újabban a tükörszimmetria és a Langlands-dualitás. Néhány területet ebben az írásban is érinteni fogunk.
Kezdjük a definícióval! A Higgs-nyaláb egy olyan ![]() pár, ahol
pár, ahol ![]() holomorf vektornyaláb, a
holomorf vektornyaláb, a ![]() -vel jelölt Higgs-mező pedig olyan holomorf
-vel jelölt Higgs-mező pedig olyan holomorf ![]() -forma, ami az
-forma, ami az ![]() endomorfizmusnyalábjából veszi fel az értékeit, továbbá kielégíti a
endomorfizmusnyalábjából veszi fel az értékeit, továbbá kielégíti a ![]() összefüggést.
összefüggést.
A legegyszerűbb esetekben a szóban forgó vektornyaláb komplex vonalnyaláb, míg a Higgs-mező holomorf 1-forma. Tekintsünk egy nem-abeli példát! Legyen ![]() , ahol
, ahol ![]() az a komplex vonalnyaláb, amelynek a négyzete éppen a Riemann-felület fölötti
az a komplex vonalnyaláb, amelynek a négyzete éppen a Riemann-felület fölötti ![]() kanonikus nyaláb (vagyis a holomorf
kanonikus nyaláb (vagyis a holomorf ![]() -formák nyalábja). Az
-formák nyalábja). Az ![]() vektornyalábon lévő Higgs-mező ekvivalens egy
vektornyalábon lévő Higgs-mező ekvivalens egy ![]() nyalábleképezéssel. Így ezzel Higgs-mezők egy, kvadratikus differenciálok által paraméterezett családját kapjuk
nyalábleképezéssel. Így ezzel Higgs-mezők egy, kvadratikus differenciálok által paraméterezett családját kapjuk ![]() felett, vagyis:
felett, vagyis:
ahol ![]() a
a ![]() vonalnyaláb szelése és
vonalnyaláb szelése és ![]() pedig a
pedig a ![]() triviális nyaláb identitás szelése.
triviális nyaláb identitás szelése.
A Hodge-elméletben egy Riemann-sokaság de Rham kohomológiaosztályainak reprezentálására harmonikus differenciálformákat használunk, míg egy Hermite-féle sokaság (jelölje ![]() ) Dolbeault kohomológia osztályait a
) Dolbeault kohomológia osztályait a ![]() -harmonikus formák reprezentálják. Ha az
-harmonikus formák reprezentálják. Ha az ![]() -en létezik Kähler-metrika, akkor a valós és a komplex elmélet kompatibilis. Ez összekapcsolja a topologikus és a holomorf adatokat az
-en létezik Kähler-metrika, akkor a valós és a komplex elmélet kompatibilis. Ez összekapcsolja a topologikus és a holomorf adatokat az![]() sokaságon, és feltár egy további struktúrát a topologikus oldalon, pontosabban a
sokaságon, és feltár egy további struktúrát a topologikus oldalon, pontosabban a ![]() kohomológiacsoportokon. Például
kohomológiacsoportokon. Például ![]() -re azt kapjuk, hogy:
-re azt kapjuk, hogy:
Holomorf tekintetben ![]() leírja az
leírja az ![]() feletti holomorf vonalnyalábok deformációját, míg
feletti holomorf vonalnyalábok deformációját, míg ![]() a holomorf
a holomorf ![]() -formák tere. Így a holomorf adat egy
-formák tere. Így a holomorf adat egy ![]() ) párból jön, ahol
) párból jön, ahol ![]() vonalnyaláb
vonalnyaláb ![]() pedig Higgs-mező, vagyis együtt egy abeli Higgs-nyalábot határoznak meg. Topologikus szemszögből
pedig Higgs-mező, vagyis együtt egy abeli Higgs-nyalábot határoznak meg. Topologikus szemszögből ![]() modellezi a
modellezi a ![]() -ből
-ből ![]() -ba menő homomorfizmusok terének érintőterét, ami ugyanaz, mint az
-ba menő homomorfizmusok terének érintőterét, ami ugyanaz, mint az ![]() feletti lapos komplex vonalnyalábok tere.
feletti lapos komplex vonalnyalábok tere.
A nem-abeli elméletben kicseréljük ![]() -ot egy nemkommutatív Lie-csoportra, egészen pontosan valamely
-ot egy nemkommutatív Lie-csoportra, egészen pontosan valamely ![]() csoportra. A Hodge-elmélet topologikus vonatkozásában a
csoportra. A Hodge-elmélet topologikus vonatkozásában a ![]() fundamentális csoport
fundamentális csoport ![]() -reprezentációit kapjuk, vagy ekvivalens módon: az
-reprezentációit kapjuk, vagy ekvivalens módon: az ![]() feletti lapos vektornyalábokat. Corlette és Donaldson tétele az elmélet harmonikus aspektusáról ad számot: ha
feletti lapos vektornyalábokat. Corlette és Donaldson tétele az elmélet harmonikus aspektusáról ad számot: ha ![]() reprezentációja teljesen reducibilis, akkor a megfelelő lapos nyaláb (jelölje
reprezentációja teljesen reducibilis, akkor a megfelelő lapos nyaláb (jelölje ![]() ) ellátható harmonikus metrikák egy családjával (ehhez a Laplace-egyenlet egy megfelelő általánosítását kell megoldani). A másik oldalon, a holomorf interpretáció azt a tényt használja fel, hogy egy nyalábon a lapos struktúrák zérus görbületű konnexiókkal vannak definiálva. A harmonikus metrika két részre vágja a lapos konnexiókat: egy ferdén önadjungált (unitér) és egy önadjungált részre. Az előbbi antiholomorf komponense egy holomorf struktúrát ad meg
) ellátható harmonikus metrikák egy családjával (ehhez a Laplace-egyenlet egy megfelelő általánosítását kell megoldani). A másik oldalon, a holomorf interpretáció azt a tényt használja fel, hogy egy nyalábon a lapos struktúrák zérus görbületű konnexiókkal vannak definiálva. A harmonikus metrika két részre vágja a lapos konnexiókat: egy ferdén önadjungált (unitér) és egy önadjungált részre. Az előbbi antiholomorf komponense egy holomorf struktúrát ad meg ![]() -n, míg utóbbi egy holomorf, endomorfizmus értékű
-n, míg utóbbi egy holomorf, endomorfizmus értékű ![]() -formát definiál, vagyis egy
-formát definiál, vagyis egy ![]() Higgs-mezőt. Így az
Higgs-mezőt. Így az ![]() holomorf adatok egy Higgs-nyalábot határoznak meg.
holomorf adatok egy Higgs-nyalábot határoznak meg.
A következőkben áttekintjük a Higgs-nyalábok néhány jellemzőjét. Kezdjük Hitchin és Simpson tételével, amely kimondja, hogy amennyiben egy Higgs-nyalábhoz a fentiek szerint egy harmonikus metrikát rendelünk, akkor a nyalábnak ki kell elégítenie egy bizonyos stabilitási feltételt. Mindez, Corlette iménti tételével együtt, az ![]() Kähler-sokaság feletti stabil Higgs-nyalábok és
Kähler-sokaság feletti stabil Higgs-nyalábok és ![]() irreducibilis
irreducibilis ![]() -reprezentációi között ad egy megfeleltetést. Ez az állítás Narasimhan és Seshadri vektornyalábokra vonatkozó híres tételének, illetve annak Donaldson, Uhlenbeck és Yau általi általánosításának Higgs-nyalábos változata.
-reprezentációi között ad egy megfeleltetést. Ez az állítás Narasimhan és Seshadri vektornyalábokra vonatkozó híres tételének, illetve annak Donaldson, Uhlenbeck és Yau általi általánosításának Higgs-nyalábos változata.
A Higgs-nyalábok fontos jellemzője egy ![]() -hatás létezése, melyet a
-hatás létezése, melyet a ![]() módon definiálunk. A Higgs-nyalábok e hatás által fixen hagyott izomorfizmusosztályai a Hodge-struktúra komplex variációi (ez áll Simpson doktori értekezésének középpontjában). Utóbbiakon keresztül a Higgs-nyalábok erős megszorításokat adnak kompakt Kähler-sokaságok lehetséges fundamentális csoportjaira.
módon definiálunk. A Higgs-nyalábok e hatás által fixen hagyott izomorfizmusosztályai a Hodge-struktúra komplex variációi (ez áll Simpson doktori értekezésének középpontjában). Utóbbiakon keresztül a Higgs-nyalábok erős megszorításokat adnak kompakt Kähler-sokaságok lehetséges fundamentális csoportjaira.
A Higgs-nyalábok másik központi tulajdonsága, hogy folytonos paramétereik vannak, vagyis olyan családokat alkotnak, amelyeket egy geometriai tér (valójában egy kvázi-projektív varietás) pontjai paramétereznek. Ez a jelenség akként ismert, hogy a Higgs-nyalábok egy modulusteret alkotnak. Bizonyos stabilitási tulajdonságtól függően, az ilyen terek konstruálásának egyik módját Mumford geometriai invariánselmélete (GIT) adja. Ha ![]() Riemann-felület (amit mostantól végig felteszünk), akkor a korábban említett stabilitási tulajdonság pontosan megfelel a GIT-beli stabilitási fogalomnak. A nem-abeli Hodge-elmélet lényege, hogy így az
Riemann-felület (amit mostantól végig felteszünk), akkor a korábban említett stabilitási tulajdonság pontosan megfelel a GIT-beli stabilitási fogalomnak. A nem-abeli Hodge-elmélet lényege, hogy így az ![]() Riemann-felület fölötti stabil Higgs-nyalábok modulustere és
Riemann-felület fölötti stabil Higgs-nyalábok modulustere és ![]() irreducibilis
irreducibilis ![]() -reprezentációinak modulustere azonosítható. A megfelelő abeli elméletben minden Higgs-nyaláb stabil, és a holomorf
-reprezentációinak modulustere azonosítható. A megfelelő abeli elméletben minden Higgs-nyaláb stabil, és a holomorf ![]() -formák tere a vonalnyalábok infinitezimális deformációs terének duálisa. Így a modulustér az
-formák tere a vonalnyalábok infinitezimális deformációs terének duálisa. Így a modulustér az ![]() Jacobi-varietás koérintőnyalábja lesz (
Jacobi-varietás koérintőnyalábja lesz (![]() — a ford.). Az ennek megfelelő reprezentációk modulustere pedig a
— a ford.). Az ennek megfelelő reprezentációk modulustere pedig a ![]() karaktervarietással lesz egyenlő.
karaktervarietással lesz egyenlő.
A modulustérnek egy harmadik leírása is adható, amikor elemeire a Hitchin-egyenletek megoldásaiként gondolunk. A Hitchin-egyenletek a ![]() Higgs-mezőre és egy, az
Higgs-mezőre és egy, az ![]() nyaláb holomorf struktúrájával kompatibilis
nyaláb holomorf struktúrájával kompatibilis ![]()
![]() -konnexióra vonatkozó mérceelméleti egyenletek:
-konnexióra vonatkozó mérceelméleti egyenletek:
![\begin{equation*}\begin{aligned}
F_A + \left[ \phi,\phi^{*} \right] &=0, \\
\mathsf{d}_A'' \phi &=0.
\end{aligned}
\end{equation*}](/images/stories/latex/d22d7bb1800b31e828be8e3b44690089_miisegyhiggsnyalab/img32.png)
Az egyenletekben ![]() az
az ![]() konnexió görbülete,
konnexió görbülete, ![]() pedig a
pedig a ![]() kovariáns deriváltjának antiholomorf része. Hitchin olyan instantonok (anti-önduális egyenletek megoldásai) vizsgálatával jutott ezekhez az egyenletekhez, amelyek egy négydimenziós tér kétdimenziós szimmetriacsoportjával való hatására invariánsak. Az egyenletek egyszerre fejezik ki az
kovariáns deriváltjának antiholomorf része. Hitchin olyan instantonok (anti-önduális egyenletek megoldásai) vizsgálatával jutott ezekhez az egyenletekhez, amelyek egy négydimenziós tér kétdimenziós szimmetriacsoportjával való hatására invariánsak. Az egyenletek egyszerre fejezik ki az ![]() formulával megadott
formulával megadott ![]() -konnexió laposságát és a kapott lapos nyalábon adott metrika harmonikusságát, összekapcsolva a lapos nyalábokat és a Higgs-nyalábokat a fenti értelemben.
-konnexió laposságát és a kapott lapos nyalábon adott metrika harmonikusságát, összekapcsolva a lapos nyalábokat és a Higgs-nyalábokat a fenti értelemben.
A négydimenziós eredet és az egyenletek szerkezete megmagyarázza a modulustér hiperkähler- struktúráját. Utóbbi egy olyan Riemann-metrika, ami Kähler-metrika három különböző komplex struktúrával is, amelyeket a kvaternió-azonosságokat kielégítő ![]() ,
, ![]() és
és ![]() operátorok definiálnak. A Riemann-felület feletti Higgs-nyalábok modulustere (jelölje
operátorok definiálnak. A Riemann-felület feletti Higgs-nyalábok modulustere (jelölje ![]() ) egy nemkompakt hiperkähler-sokaság. A
) egy nemkompakt hiperkähler-sokaság. A ![]() -hatás megszorítása az
-hatás megszorítása az -ra valamelyik Kähler-formára vonatkozó Hamilton-féle hatás lesz a modulustéren, a hozzá tartozó szimplektikus momentumleképezés pedig a Higgs-mező
![]() -normájából jön. Utóbbi leképezés egy perfekt Bott—Morse-függvényt határoz meg a modulustéren, és erős eszközt ad a modulustér topológiájának tanulmányozására.
-normájából jön. Utóbbi leképezés egy perfekt Bott—Morse-függvényt határoz meg a modulustéren, és erős eszközt ad a modulustér topológiájának tanulmányozására.
Amellett, hogy a Higgs-mező egy kitüntetett Morse-függvényt biztosít, felelős a modulustér egy lényeges jellemzőjéért: a Hitchin-fibrálás létezéséért. Mivel ![]() egy nyaláb fibrumainak endomorfizmusaiból veszi az értékeit, ezért kiszámítható a
egy nyaláb fibrumainak endomorfizmusaiból veszi az értékeit, ezért kiszámítható a ![]() kifejezés. Ennek a karakterisztikus polinomnak az együtthatói definiálják a Hitchin-fibrálást:
kifejezés. Ennek a karakterisztikus polinomnak az együtthatói definiálják a Hitchin-fibrálást:
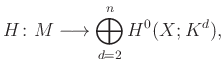
ahol ![]() a kanonikus nyaláb
a kanonikus nyaláb ![]() -en. A Hitchin-fibrálás képhalmaza egy
-en. A Hitchin-fibrálás képhalmaza egy ![]() dimenziójú vektortér, generikus fibruma egy Abel-varietás, pontosabban egy ún. spektrál görbe Jacobi-varietása. Ez egy algebrai teljesen integrálható rendszerre szolgáltat példát.
dimenziójú vektortér, generikus fibruma egy Abel-varietás, pontosabban egy ún. spektrál görbe Jacobi-varietása. Ez egy algebrai teljesen integrálható rendszerre szolgáltat példát.
A Hitchin-fibrálás egy kitüntetett szelése, melynek képe a ![]() csoport
csoport -beli reprezentációinak modulusterének egy komponensét adja, egy
![]() dimenziós komplex cellát alkot, ami
dimenziós komplex cellát alkot, ami ![]() -re a felület Teichmüller-terének felel meg. A Higgs-nyalábok pedig éppen a korábban tárgyalt
-re a felület Teichmüller-terének felel meg. A Higgs-nyalábok pedig éppen a korábban tárgyalt ![]() rangú példák. Az (1) képletben a
rangú példák. Az (1) képletben a ![]() feltevéssel élve, majd a Hitchin-egyenletek egzisztenciatételét alkalmazva, a Riemann-felületek uniformizációs tételének új bizonyítását nyerjük.
feltevéssel élve, majd a Hitchin-egyenletek egzisztenciatételét alkalmazva, a Riemann-felületek uniformizációs tételének új bizonyítását nyerjük.
Gyakorlatilag minden fent leírt eszköz alkalmazható, ha az ![]() csoportot kicseréljük egy
csoportot kicseréljük egy ![]() komplex, féligegyszerű Lie-csoportra. Az így nyert
komplex, féligegyszerű Lie-csoportra. Az így nyert ![]() -Higgs-nyaláb elmélet holomorf eszközöket nyújt a
-Higgs-nyaláb elmélet holomorf eszközöket nyújt a ![]() csoport
csoport ![]() -beli, illetve
-beli, illetve ![]() valós formáiba való reprezentációinak tanulmányozásához. Ez annak a jele, hogy még sokat tanulhatunk a Higgs-nyalábok elméletéből. Például Higgs-nyalábok, a topologikus mezőelméleten keresztül, szerepet játszanak a geometriai Langlands-program Kapustin—Witten interpretációjában. Végül megjegyezzük, hogy a Hitchin-egyenletek itt egy kétdimenziós szimmetriát indukálnak, épp úgy, amint Hitchin eredetileg származtatta az egyenleteit.
valós formáiba való reprezentációinak tanulmányozásához. Ez annak a jele, hogy még sokat tanulhatunk a Higgs-nyalábok elméletéből. Például Higgs-nyalábok, a topologikus mezőelméleten keresztül, szerepet játszanak a geometriai Langlands-program Kapustin—Witten interpretációjában. Végül megjegyezzük, hogy a Hitchin-egyenletek itt egy kétdimenziós szimmetriát indukálnak, épp úgy, amint Hitchin eredetileg származtatta az egyenleteit.
Irodalomjegyzék
- [1] Az első két úttörő munka: N. J. HITCHIN, The self-duality equations on a Riemann surface, Proc. London Math. Soc. (3), 55 (1987) 59—126; és C. T. SIMPSON, Higgs bundles and local systems, Publ. Math. I. H. E. S. 75 (1992) 5—95.
- [2] A későbbi eredményekhez lásd: S. BRADLOW, O. GARCíA-PRADA és P. B. GOTHEN, Surface group representations and
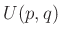 -Higgs bundles, J. Diff. Geom. 64 (2003) 111—170; és R. DONAGI és T. PANTEV, Langlands duality for Hitchin systems, Invent. Math. (3) 189 (2012) 653—735.
-Higgs bundles, J. Diff. Geom. 64 (2003) 111—170; és R. DONAGI és T. PANTEV, Langlands duality for Hitchin systems, Invent. Math. (3) 189 (2012) 653—735.
Steven B. Bradlow, Oscar Gracía-Prada, Peter B. Gothen
A cikk eredetileg a Notices of the American Mathematical Society folyóirat What is... rovatában jelent meg 2007-ben. Ez a fordítás a szerzők és az AMS engedélyével jelenik meg. A fordítást készítette: Ivanics Péter.