Mi is ... egy pszeudo-holomorf görbe?

Mikhail Gromov A pszeudo-holomorf (vagy $J$ -holomorf) görbe fogalmát Gromov vezette be 1986-ban, amivel gyökeresen alakította át a szimplektikus topológiát, és több más közeli diszciplínára, például algebrai geometriára, húrelméletre, 4-sokaságok elméletére volt döntő hatással; ezekre később még visszatérünk.

A „görbe” – mondjuk egy síkgörbe – mindannyiunk számára ismerős fogalom. Két módon is megadhatunk egy síkgörbét: akár mint az $f(x,y)=0$ egyenlet megoldáshalmazát valamilyen $f$ függvényre, akár az $x=x(t), y=y(t)$ paraméterezéssel. A körvonalat például megadhatjuk az $x^2+y^2=1$ egyenlettel vagy az $x=\cos t, y=\sin t$ paraméterezéssel. Egy további ismerős fogalom görbék egy „családja”, például a sík összes egyeneseinek családja.

Görbéket mind a differenciálgeometriában, mind az algebrai geometriában hosszú ideje tanulmányoznak. A klasszikus elmélet számunkra most érdekes változata a „komplex” vagy „holomorf” görbék elmélete. Legegyszerűbb változatában helyettesítsük az $x,y$ valós változókat a $z,w$ komplex változókkal; így egy komplex görbét kapunk a komplex síkon. A $z^2 + w^2 = 1$ egyenlet például egy komplex görbét ad meg. Hasonlóan, tekinthetünk paraméterezett komplex görbéket, melyeket a $z = z(\tau ), w = w(\tau )$ egyenletek adnak meg, ahol $z(\tau )$ és $w(\tau )$ holomorf függvényei a $\tau$ komplex változónak. Általánosabban, komplex sokaságokban is tekinthetünk komplex görbéket, melyeket Riemann-sokaságokon értelmezett holomorf függvények parametrizálnak.

De mi is egy holomorf leképezés? Vegyük először a legegyszerűbb esetet, amikor az $f$ leképezés ${\bf {C}}$ -ből ${\bf {C}}$ -be képez: ekkor egyszerűen egy holomorf függvény. A holomorf tulajdonságot a Cauchy-Riemann egyenlet teljesülése jelenti, vagyis hogy

$\begin{displaymath} \frac{\partial f}{\partial {\overline {z}}}=0. \end{displaymath}$ Az egyenlet azt fejezi ki, hogy az $f$ deriváltja (többváltozós függvénytani értelmében) minden pontban egy ${\bf {C}}$ -ből ${\bf {C}}$ -be vezető komplex lineáris leképezés. A fogalom természetesen terjed ki majdnem-komplex sokaságokra is. Legyen tehát $M$ egy $2n$ -dimenziós differenciálható (vagy más néven sima) sokaság. Egy $M$ -en értelmezett majdnem-komplex struktúra egy $J_x\colon T_xM\to T_xM$ leképezés-család mely minden $x\in M$ pontra a $T_xM$ érintőtéren teljesíti a $J_x^2=-1$ egyenletet, és $x\in M$ -től differenciálható módon függ. Röviden, $J$ az érintőtereket komplex vektorterekké teszi. Minden komplex sokaságon van egy természetes majdnem-komplex struktúra, de a megfordított állítás már nem igaz $n>1$ esetén: egy integrálhatósági feltétel karakterizálja azokat a speciális majdnem-komplex struktúrákat, melyek komplex struktúrából származnak. Számos olyan sokaság létezik, melyen ugyan van majdnem-komplex struktúra, de egyáltalán nem látható el komplex struktúrával.

A pszeudo-holomorf görbe fogalma a holomorf görbe természetes módosítása arra az esetre, amikor a bennfoglaló sokaság csak majdnem-komplex. Pontosabban, vegyünk egy $\Sigma$ Riemann-felületet, egy $(M,J)$ majdnem-komplex sokaságot és egy $f\colon \Sigma \to M$ differenciálható leképezést melyre minden $\sigma \in \Sigma$ esetén teljesül, hogy a $\begin{displaymath} df_{\sigma}\colon T _{\sigma} \Sigma \to T_{f(\sigma )}M \end{displaymath}$ derivált leképezés komplex lineáris az adott komplex struktúrákkal az érintőtereken. Konkrétan, tekintsük a $\Sigma ={\bf {C}}$ , $M={\bf {C}}^n$ és ezen egy $J$ általános majdnem-komplex struktúra esetét. Lineáris algebrai érveléssel látható, hogy az ${\bf {R}}$ -lineáris $J\colon {\bf {C}}^n \to {\bf {C}}^n$ leképezések melyek a $J^2=-1$ egyenletet is teljesítik, az $n\times n$ -es komplex mátrixok (melyeket $\mu =(\mu _{\alpha \beta })$ -val jelölünk) egy nyílt részhalmazát alkotják. 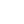A majdnem-komplex struktúra tehát egy $\mu (z)$ ( $z\in {\bf {C}}^n$ ) mátrix-értékű függvénnyel írható le. Egy pszeudo-holomorf görbe a következő parciális differenciálegyenlet megoldásaként adható meg:

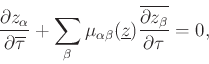$\begin{displaymath} \frac{\partial z_{\alpha}}{\partial {\overline {\tau}}}+ \s... ...)\frac{{\overline {\partial z_{\beta}}}}{\partial \tau }=0, \end{displaymath}$ az egyenlet a szokásos Cauchy-Riemann egyenlet deformációjának tekinthető a ${\underline {z}}(\tau )=(z_{\alpha }(\tau))$ vektorértékű függvényre.

Azzal, hogy majdnem-komplex struktúrákat tekintünk, a klasszikus holomorf görbe-elméletnél szélesebb és rugalmasabb világban találjuk magunkat. A klasszikus elmélet számos vetülete nem nagyon változik, amennyiben ilyen irányba terjesztjük azt ki. Röviden azt mondhatjuk, hogy a pszeudo-holomorf görbék lokális elmélete nagyon hasonlít a holomorf görbék elméletéhez. Ebben a kontextusban a lokálisnak két értelmezése is lehetséges: akár úgy, hogy a problémát lokálisan vizsgáljuk az $M$ sokaságban vagy lokálisan a leképezések terében. Fontos kiemelni, hogy görbéket vizsgálunk és nem magasabb dimenziós objektumokat. Ugyan bármely $N,M$ majdnem-komplex sokaság-párra értelmezhető egy $f\colon N\to M$ leképezés (pszeudo-)holomorfsága, de amint $N$ valós dimenziója több mint 2, ez nem túl hasznos fogalom. Egy általános majdnem-komplex $N$ sokaság esetén, melynek dimenziója több mint 2, például még lokálisan sem létezik nem-konstans (pszeudo)holomorf leképezés $M$ -be – épp ez az integrálhatósági feltétel forrása komplex sokaságokra.

Állításunk egy pontosabb megfogalmazása a következő: egy $\Sigma$ kompakt Riemann-sokaság esetén egy adott $f\colon \Sigma \to (M,J)$ pszeudo-holomorf görbe deformációinak elméletét egy nem-lineáris Fredholm-elmélet írja le. Ez nagyjából azt jelenti, hogy a deformációkat egy véges dimenziós sokaság, egy ${\mathcal {M}}$ modulustér paraméterezi, melynek dimenzióját topológikus adatokból lehet kiszámolni. Továbbá ez a modulustér simán változik mind a $J$ majdnem-komplex struktúra mind a $\Sigma$ -n rögzített Riemann-sokaság struktúra függvényeként. Vegyük például azt az esetet, amikor $M$ a komplex projektív tér (annak standard komplex struktúrájával), $\Sigma$ pedig a Riemann-gömb. Ekkor minden $M$ -beli „egyenes” (a szó projektív geometriai értelmében) valamint egy egyenes minden paraméterezése egy pszeudo-holomorf görbét ad. Következésképp az ${\mathcal {M}}$ modulustér a duális sík felett egy $PGL(2, {\bf {C}})$ -fibrumú nyaláb (a $PGL(2, {\bf {C}})$ csoport a Möbius-leképezések csoportja). A nem-lineáris Fredholm-elmélet azt mutatja, hogy ha deformáljuk a majdnem-komplex struktúrát, akkor ugyan valószínűleg nem tudjuk majd a pszeudo-holomorf görbéket expliciten leírni, de hasonló általános tulajdonságokkal rendelkező modulusteret kapunk.

Gromov észrevétele az volt, hogy a Fredholm elmélet által a pszeudo-holomorf leképezésekről adott lokális kép egy globális képpé alakítható, feltéve hogy $M$ majdnem-komplex struktúrája egy szimplektikus struktúrával kompatibilis. Emlekézzünk, hogy egy szimplektikus struktúrát egy olyan $\omega$ külső 2-forma ad meg, mely két feltételt teljesít. Az első feltétel pontonkénti és algebrai: a sokaság minden pontjában $\omega$ egy nem-elfajuló anti-szimmetrikus forma $M$ abban a pontban vett érintőterén. A másik feltétel globálisabb és differenciálgeometriai: az $\omega$ 2-forma zárt. Akkor mondjuk, hogy $J$ kompatibilis $\omega$ -val, ha az érintővektorokon értelmezett

$\begin{displaymath} g(v, w) = \omega (v, Jw) \end{displaymath}$ bilineáris forma szimmetrikus és pozitív definit. Ebben az esetben $g$ egy $M$ -en értelezett Riemann metrika lesz. Legyen $f\colon \Sigma \to M$ egy pszeudo-holomorf leképezés. Az

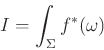$\begin{displaymath} I=\int _{\Sigma }f^*(\omega) \end{displaymath}$ integrálra ekkor kétféleképp is gondolhatunk. Egyrészt, a pontonkénti kompatibilitás miatt $I$ lényegében az $f$ képének területe, melyet a $g$ metrika segítségével mérünk. Másrészt viszont, mivel $\omega$ zárt forma, az $I$ mennyiség az $f$ leképezés topologikus (homotopikus) invariánsa. Következésképp ebben az esetben pszeudo-holomorf görbék területe egy egyszerű topologikus adattal határozható meg. Ezt a tulajdonságot használva Gromov egy részleges kompaktsági tulajdonságot tudott bizonyítani a modulusterekre. Vegyük például a Riemann gömbről a komplex projektív síkba mutató leképezéseket. Ha megengedjük, hogy a majdnem-komplex struktúrát tetszőleges mértékben és tetszőleges irányban deformáljuk, akkor nem sokat tudunk mondani, hiszen a pszeudo-holomorf görbék nagyon bonyolult módokon degenerálódhatnak ahogy a majdnem-komplex struktúrát deformájuk, és a leképezések akár el is „tűnhetnek”. De ha csak olyan majdnem-komplex struktúrákat engedünk meg, melyek egy szimplektikus formával kompatibilisek, akkor a görbék nem tudnak degenerálódni, mert területüket kontrollálni tudjuk. Ebben az esetben Gromov valójában megmutatta, hogy a görbéknek meg kell maradniuk, akármilyen nagy deformációt is alkalmazunk.

E két tulajdonság – a Fredholm elmélet és a kompaktság – adja Gromov elméletének alapjait, mely keretében pszeudo-holomorf görbéket használunk szimplektikus topológiai kérdések megválaszolására. Ezeket a görbéket két alapvető módon használhatjuk. Az első megközelítésben mint geometrikus ‚szondákat’, melyekkel felderíthető a szimplektikus sokaság: például Gromov egy eredménye szerint (melyet később Taubes terjesztett ki) a komplex projektív síkon egyetlen szimplektikus struktúra létezik, melyet úgy lehet belátni, hogy a sokaságot végigseperjük „egyenesekkel” (vagyis olyan pszeudo-holomorf görbékkel, melyeknek ugyanolyan topologikus tulajdonságaik vannak, mint az egyeneseknek a standard esetben). A második megközelítésben a görbék numerikus invariánsok forrásai: ezek az úgynevezett Gromov-Witten invariánsok. A legegyszerűbb esetben, amikor a modulustér 0-dimenziós és véges sok pontból áll, egy egész értékű invariánst kapunk pusztán ezen pontok megszámolásával. E második irány fejlődött legdinamikusabban Gromov cikkének megjelenése után. A Floer homológiák elmélete is hasonló alapokon nyugszik; ebben az esetben olyan pszeudo-holomorf görbéket kell számolni, melyek pereme egy rögzített Lagrange féle részsokaságra képződik. Ez az elmélet vezet el a Fukaya kategória fogalmához. A négydimenziós esetben Taubes felfedezte, hogy a Gromov-Witten invariánsok megegyeznek a Seiberg-Witten invariánsokkal, melyeket teljesen más módon definiálhatunk. Abban az esetben, amikor a sokaság valójában komplex, mondjuk egy algebrai varietás, az invariánsok az algebrai geometria klasszikus leszámlálási kérdéseihez kapcsolódnak. Ugyanezen invariánsok, a Feynman integrálokon keresztül, feltűnnek a topologikus húrelméletben is. Ez a megközelítés teljesen új látásmódot, és csodálatos és érzékeny algebrai struktúrákat, kvantum kohomológiákat eredményezett. A sokaság Fukaya kategóriája pedig, Kontsevich munkája nyomán, a tükörszimmetria jelenségéhez is szorosan kapcsolódik.

Irodalom:

Dusa McDuff és Dietmar Salamon, $J$ -holomorphic Curves and Symplectic Topology, Amer. Math. Soc. Colloq. Publ., Vol. 52, 2004.

______________________________

Simon Donaldson az Imperial College (London) Royal Society Research professzora. A cikk eredetileg az American Mathematical Society Notices folyóiratának 2005. októberi számában jelent meg a What is …? rovatban. Ez a fordítás a szerző és az AMS engedélyével jelenik meg. A fordítást Stipsicz András készítette.