A késleltetett visszacsatolás jelenségét mindenki tapasztalta már, pl. zuhanyozás során. Tegyük fel, hogy egy keverőcsap elforgatásával változtatjuk a csapból kimenő víz hőmérsékletét, továbbá a víz hőfokának változása arányos a csap elforgatásának a szögével. Legyen ![]() a zuhanyozáshoz optimális vízhőmérséklet,
a zuhanyozáshoz optimális vízhőmérséklet, ![]() pedig a csapból kimenő víz hőmérséklete a
pedig a csapból kimenő víz hőmérséklete a ![]() időben. Feltesszük, hogy a csap elforgatásának a sebessége arányos az általunk érzékelt vízhőfok és az optimális vízhőfok eltérésével. Vegyük észre, hogy a
időben. Feltesszük, hogy a csap elforgatásának a sebessége arányos az általunk érzékelt vízhőfok és az optimális vízhőfok eltérésével. Vegyük észre, hogy a ![]() időpillanatban azt a vízhőmérsékletet érzékeljük, amely a csapból
időpillanatban azt a vízhőmérsékletet érzékeljük, amely a csapból ![]() idővel korábban, a
idővel korábban, a ![]() időpillanatban folyt ki. Ennek oka az, hogy a csaptól a zuhanyrózsáig egy
időpillanatban folyt ki. Ennek oka az, hogy a csaptól a zuhanyrózsáig egy ![]() hosszúságú cső vezet, amelyen a víz
hosszúságú cső vezet, amelyen a víz ![]() idő alatt folyik át. A fentiek alapján a
idő alatt folyik át. A fentiek alapján a ![]() hőmérsékletre a
hőmérsékletre a
| (1) |
differenciálegyenletet kapjuk, ahol ![]() arányossági állandó. Előfordulhat, hogy a csap elforgatásának a sebessége nem egyenesen arányos, hanem egy nemlineáris függvénye az érzékelt vízhőfok és az optimális vízhőfok eltérésének. Ekkor a modellegyenlet
arányossági állandó. Előfordulhat, hogy a csap elforgatásának a sebessége nem egyenesen arányos, hanem egy nemlineáris függvénye az érzékelt vízhőfok és az optimális vízhőfok eltérésének. Ekkor a modellegyenlet
| (2) |
alakú, ahol ![]() olyan folytonos függvény, amelyre az
olyan folytonos függvény, amelyre az ![]() feltétel teljesül
feltétel teljesül ![]() esetén.
esetén.
A fenti példa egy tipikus visszacsatolási mechanizmus. Egy folyamat kimenetét felhasználjuk arra, hogy a folyamat változását befolyásoljuk. A kimenő adatot valamilyen visszacsatolási mechanizmus folytán visszatápláljuk (feed back) a rendszerbe. A visszacsatolás a legtöbb esetben nem azonnal történik, a mechanizmus természetéből adódóan ahhoz nem elhanyagolható időre van szükség. Ez a késleltetett visszacsatolás.
Késleltetett visszacsatolás sokféle jelenségben előfordul. Populációdinamikai modellekben az időkésleltetés adódhat pl. egy egyed felnőtté válásához szükséges időből. Idegsejt-hálózatokban, kommunikációs hálózatokban a jelek, információk átviteléhez nem elhanyagolható időre van szükség. Autókövetési és közlekedési modellekben a reakcióidő ad késleltetett visszacsatolást. Vezérlési, irányıtási feladatokban a jelátvitelhez szükséges idő és a reakcióidő együttesen eredményeznek időkésleltetést. Sok élettani jelenség modellezhető késleltetett visszacsatolást tartalmazó differenciálegyenlettel. Társadalmi, gazdasági, tanulási folyamatokban is fontos szerepe van a késleltetett visszacsatolásnak.
A késleltetett visszacsatolást modellező differenciálegyenletek az ún. funkcionál-differenciálegyenletek. Ezek a közönséges differenciálegyenletektől abban különböznek formailag, hogy bennük az ismeretlen függvény múltbeli értékei is előfordulnak. Ha bevezetjük az
jelölést, akkor az (1) egyenlet
| (3) |
alakú. Ha ![]() , akkor a megoldás
, akkor a megoldás ![]() . (Az 1. ábra néhány ilyen megoldást mutat.)
. (Az 1. ábra néhány ilyen megoldást mutat.)
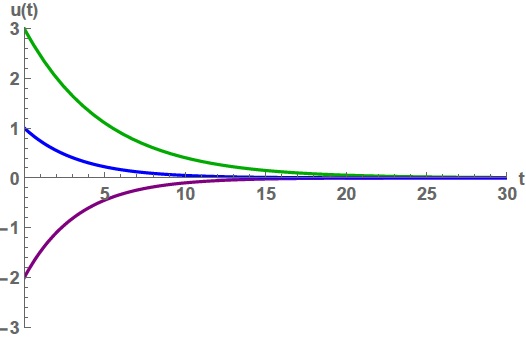
1. ábra
Ha ![]() , akkor
, akkor ![]() megadása nem elegendő
megadása nem elegendő ![]() meghatározásához
meghatározásához ![]() -ra. Ismernünk kell az
-ra. Ismernünk kell az ![]() értékeket
értékeket ![]() esetén. Ez azt jelenti, hogy az időkésleltetéses egyenletek állapottere egy függvénytér, hasonlóan a parciális differenciálegyenletekhez. A (2) egyenletnek végtelen sok lineárisan független megoldása van. Létezik végtelen sok komplex
esetén. Ez azt jelenti, hogy az időkésleltetéses egyenletek állapottere egy függvénytér, hasonlóan a parciális differenciálegyenletekhez. A (2) egyenletnek végtelen sok lineárisan független megoldása van. Létezik végtelen sok komplex ![]() úgy, hogy
úgy, hogy ![]() . Ekkor
. Ekkor ![]() komplex megoldás, valós és képzetes része,
komplex megoldás, valós és képzetes része, ![]() és
és ![]() pedig valós megoldás. Ha
pedig valós megoldás. Ha ![]() , akkor ezen megoldások mindegyike oszcillál 0 körül (lásd a 2. ábrát) , ellentétben a
, akkor ezen megoldások mindegyike oszcillál 0 körül (lásd a 2. ábrát) , ellentétben a ![]() esetben kapott monoton megoldásokkal.
esetben kapott monoton megoldásokkal.
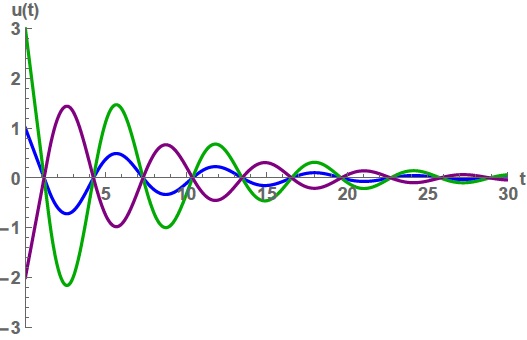
2. ábra
Speciálisan, ![]() esetén
esetén ![]() és
és ![]() periodikus megoldások (3. ábra). Ha pedig
periodikus megoldások (3. ábra). Ha pedig
akkor a 0 instabillá válik, ezt szemlélteti a 4. ábra.
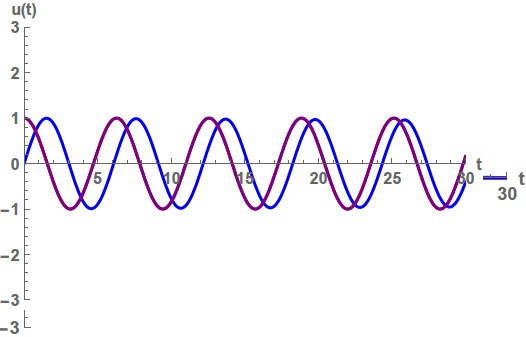
3. ábra
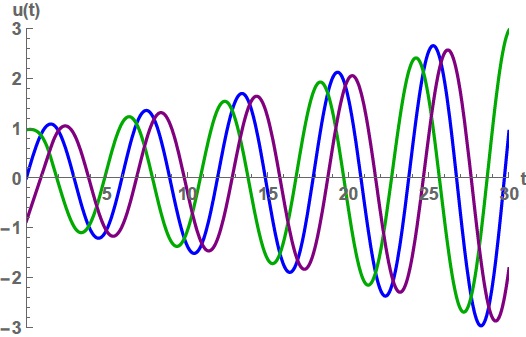
4. ábra
Késleltetett visszacsatolást tartalmazó differenciálegyenletek vizsgálata során fontos kérdés, hogy hogyan változik a megoldások szerkezete (a dinamika) a késleltetés (mint paraméter) változtatásával. Egy tipikus eredmény az, hogy van a késleltetéseknek egy ![]() növekvő sorozata úgy, hogy
növekvő sorozata úgy, hogy ![]() és
és ![]() esetén a (2) egyenletnek legalább
esetén a (2) egyenletnek legalább ![]() (eltolástól eltekintve) különböző frekvenciával oszcilláló periodikus megoldása van. Bizonyos monoton
(eltolástól eltekintve) különböző frekvenciával oszcilláló periodikus megoldása van. Bizonyos monoton ![]() függvényekre ismert, hogy pontosan
függvényekre ismert, hogy pontosan ![]() periodikus megoldás van. A
periodikus megoldás van. A ![]() eset a Wright-egyenlet, ahol
eset a Wright-egyenlet, ahol ![]() , ha
, ha ![]() . Ekkor az
. Ekkor az ![]() esetre a pontos állıtás a Wright-sejtéssel ekvivalens, az
esetre a pontos állıtás a Wright-sejtéssel ekvivalens, az ![]() eset pedig Jones-sejtésként ismert. Egyik sem teljesen megoldott.
eset pedig Jones-sejtésként ismert. Egyik sem teljesen megoldott.
Nem monoton ![]() visszacsatolási függvényre a
visszacsatolási függvényre a ![]() (
(![]() ) feltétel mellett a (2) egyenlet megoldásai által generált dinamika bonyolult, kaotikus lehet.
) feltétel mellett a (2) egyenlet megoldásai által generált dinamika bonyolult, kaotikus lehet.
Az időkésleltetés növelésével egy adott rendszer egyre bonyolultabbá válhat. Ez azonban általánosan nem érvényes. Vannak olyan rendszerek, ahol az időkésleltetés növelése egyszerűsítő, stabilizáló hatást eredményez. Bizonyos esetekben a kaotikus viselkedés kontrollálható egy alkalmas késleltetett visszacsatolási mechanizmus bevezetésével (Pyragas-kontroll).
A késleltetett visszacsatolás nem feltétlenül egyetlen időkésleltetéses tagot jelent az egyenletben. Több késleltetés, vagy eloszlásfüggvénnyel megadott késleltetés esetén kevés globális eredmény ismert.
Újabban egyre több olyan késleltetett visszacsatolást modellező egyenlet merül fel, ahol az időkésleltetés magától a megoldástól is függ. Például a pozícióját egy fix referenciaponthoz küldött és onnan visszakapott jel utazási idejéből becsülő objektum vezérlése ilyen időkésleltetést eredményez, mert a jel utazási ideje függ az objektum helyétől. Az ilyen egyenletek nem illeszthetők a klasszikus állandó késleltetéses egyenletek osztályába. Néhány alapvető eredmény már létezik, de számos nyitott kérdés van, elsősorban a megoldás-operátorok simaságával kapcsolatban.
Krisztin Tibor
Szegedi Tudományegyetem
Megjegyzések:
Szegedi matematikusok kapták a Moore-díjat - erről szól kapcsolódó cikkünk a 2016 decemberi számunkban.
Dr. Krisztin Tibor, a Szegedi Tudományegyetem oktatója lett 2016-ban a Bolyai János Matematikai Társulat Szele Tibor Emlékérmet elnyert kutatója: ez a hír is megtalálható a 2016 decemeberi számban. A Szerk.









