A matematika és fizika tudománya évszázadok óta kart karba öltve fejlődik. A fizika a matematika nyelvén fogalmazza meg törvényeit, igényei pedig hatással vannak a matematika fejlődésére. Hogyan jelenik meg ez a szoros kapcsolat az oktatásban? Támaszkodik-e a két tantárgy a másikban született „eredményekre”? Hogyan, mely területeken kapcsolódik, kapcsolható össze a két tárgy oktatása? A kapcsolódási lehetőségek ismerete segíthet-e a hatékonyabb tanításban? Ezekre a kérdésekre keresem a választ ebben a cikkben.
A matematikaórákon tanult ismeretek alkalmazására leginkább a fizikaórákon nyílik lehetőség a középiskolában. A matematika szinte minden területéről előkerülnek az ismeretek. A fizika támaszkodik ezekre, egyben segíti is a matematikaoktatást, gyakoroltatja a tanultakat. Eközben megtanít a különböző tananyagrészekben elsajátítottak összekapcsolására.
Ideális esetben a két tantárgy oktatása szinkronizálható abban a tekintetben, hogy fizikából csak a tanult matematikai ismeretekre alapozzunk. A gyakorlatban ez nem mindig működik így. Több területen találkozunk azzal a problémával, hogy fizikaórán már alkalmazás szinten kellene használni a tanulónak olyan matematikai összefüggéseket, amelyekkel a matematikaórán még alig, vagy egyáltalán nem találkozott. Mivel a fizika sok esetben „megelőzi” a matematikát, a fizikatanár rákényszerül arra, hogy bevezesse a hiányzó matematikai ismereteket, még ha kicsit nagyvonalúbban, kevésbé pontosan teszi is meg. A matematikatanítás szempontjából ez előnyös is lehet, időt nyerhetünk az alapozásnál, ha tudjuk, hogy fizikából milyen előismeretekkel rendelkeznek diákjaink. Melyek tehát ezek az ismeretek, amelyek alapozásában építhetünk a fizikaórán tanult előismeretekre? A teljesség igénye nélkül néhány terület:
Hetedik osztály elején a sebesség fogalmához kapcsolódóan találkozunk az első problémával. Matematikából hatodik osztály végén még csak ismerkedünk a mérlegelvvel, mindkét oldal azonos mennyiséggel történő növelését és csökkentését gyakorolva. A szorzás és osztás műveletekre még nem fektetünk hangsúlyt. Fizikaórán viszont a ![]() képlet alkalmazása során meg kell tanítanunk a diákot a képlet átrendezésére, hogy az
képlet alkalmazása során meg kell tanítanunk a diákot a képlet átrendezésére, hogy az ![]() és
és ![]() értékeket ki tudjuk számítani. A tanévben több ehhez hasonló szerkezetű képlettel ismerkednek meg a tanulók, így a kapcsolódó feladatokban a tanult egyenletrendezési ismeretek elmélyülhetnek.
értékeket ki tudjuk számítani. A tanévben több ehhez hasonló szerkezetű képlettel ismerkednek meg a tanulók, így a kapcsolódó feladatokban a tanult egyenletrendezési ismeretek elmélyülhetnek.
Ugyancsak hetedik osztály elején a mozgások vizsgálata során grafikont készítünk, konstans és lineáris függvény grafikonját elemezzük, sőt a változó mozgásokra térve a négyzetes úttörvény szemléltetésére a parabola grafikonját is felrajzoljuk.
A fordított arányosság a sebesség mértékegységeinek átváltása során már előkerül, de legkésőbb félévkor a forgatónyomaték fogalmát bevezetve foglalkozunk vele.
Ugyancsak kezdetektől foglalkozunk az átlag fogalmával, sőt a súlyozott átlaghoz és a harmonikus középhez vezető feladatokkal is találkoznak a tanulók.
Kilencedik osztályban a gyorsuló mozgás kapcsán a gyökvonással megoldható egyenletekkel ismerkedünk.
A vektor fogalma hetedik osztálytól nagyon fontos a fizika számára, és tizedik osztály végéig a fizika igényei megelőzik ebben a témában a matematikaórán tanultakat. Ezt a későbbiekben részletezni fogom.
Ugyancsak kilencedik osztályban év elejétől szükség van a negatív kitevőjű hatvány ismeretére.
Milyen matematikai fogalmakat, módszereket használunk tehát a fizika tanítása során? Szinte minden matematikaórán tanult ismeretet. Íme néhány főbb témakör, ami rendszeresen megjelenik a fizikaórákon:
| – Középértékek, statisztikai fogalmak |
| – Műveletek törtekkel, reciprok fogalma |
| – Hatványok, normál alak, hatványozás azonosságai, exponenciális kifejezések |
| – Arányosságok |
| – Algebrai összefüggések: nevezetes szorzatok, zárójelfelbontás |
| – Lineáris, másodfokú, négyzetgyök, exponenciális, logaritmus, trigonometrikus függvények |
| – Első-, másodfokú, négyzetgyökös, exponenciális, egyszerű trigonometrikus egyenletek, elsőfokú egyenletrendszerek |
| – Geometriai ismeretek: terület-, térfogatszámítás, Pitagorasz-tétel, hasonlóság, egyenlő nagyságú szögek speciális helyzetei, hegyesszögek szögfüggvényei |
| – Vektorok |
A fentieket a középszintű fizika tananyag elsajátításához szükséges ismeretekből válogattam, de minél magasabb szinten tanuljuk a fizikát, annál komolyabb matematikai ismeretekre lesz szükségünk (differenciál- és integrálszámítás, valószínűségszámítás, statisztika, stb.)
A továbbiakban konkrét példákon keresztül mutatom be, hogy milyen lehetőségeket ad hozzá a matematika tanításához a fizika.
Fogalmak alapozása, előkészítése
Több területet is említettem, ahol a fizika olyan matematikai fogalmakat használ, amelyeket a matematikaoktatás még nem alapozott meg kellőképpen. Mivel ilyenkor a fizikatanár rákényszerül ezek valamilyen szintű bevezetésére, ezekre az előismeretekre a matematikaórán már építhetünk. Ebből a szempontból külön figyelmet érdemes fordítani a vektorok témakörre. Szinte minden alapfogalma, művelete, minden ide kapcsolódó módszere előbb jelenik meg a fizikaoktatásban, mint matematikaórákon. Ha megismerjük, hogy a fizika az ide tartozó fogalmakat, szabályokat milyen folyamatokon keresztül vezeti be, akkor a matematikaórákon ennek már csak a pontosítása a feladatunk. Tapasztalatból mondhatom, hogy ezzel rengeteg időt tudunk megspórolni. Nézzük ezért lépésről lépésre, hogy fizikaórán milyen mélységig foglalkoznak a tanulók a vektorokhoz kapcsolódó ismeretekkel!
A sebesség és az erő fogalmainak ismertetésekor a diákok már hetedik osztályban találkoznak a vektor fogalmával. A vektor nekik ekkor egy olyan fizikai mennyiséget jelent, aminek nem csak nagysága, hanem iránya is van. Ezeket a mennyiségeket az ábrákon nyíllal jelöljük. Az erőfogalom megismerésekor bevezetjük az erő hatásvonala (az erővektorra illeszkedő egyenes) és támadáspontja fogalmakat. Később ebből matematikaórákon származhat bonyodalom. A vektoroknak ugyanis kezdő- és végpontjuk nincsen, ebből adódóan a párhuzamos, egyenlő hosszúságú, megegyező irányú vektorok hatása matematikában ugyanaz. Fizikában viszont nagy hangsúlyt kell fektetnünk arra, hogy az erővektornak hol van a támadáspontja, hiszen ettől függően más hatást eredményezhet.
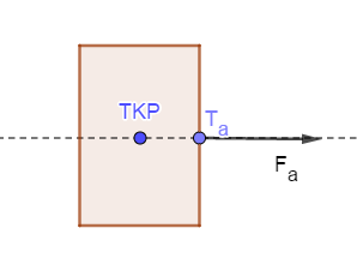
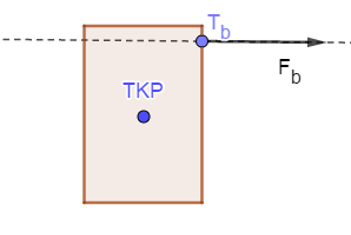
Az ábra két egyenlő erővektor (Fa, ill. Fb) hatását mutatja ugyanazon a testen, ha a támadáspontjuk (Ta, ill. Tb) különböző. Az a) esetben az erő csak gyorsítja a testet, míg a b) esetben az erőnek forgató hatása is van. (TKP jelöli a tömegközéppontot.)
Amíg fizikaórán azt tanítjuk, hogy az erővektor hatásvonala mentén eltolható, mert ugyanazt a hatást eredményezi, addig matematikaórán a tetszőleges eltolással egymásba mozgatható vektorokat tekintjük egyenlőnek. Amikor a középiskolai oktatásban a vektorok témához érkezünk, tudnunk kell, hogy a vektorfogalom általánosítását megnehezíthetik ezek az eltérések. Fontos tehát, hogy ismerjük és tisztázzuk ezeket a különbségeket.
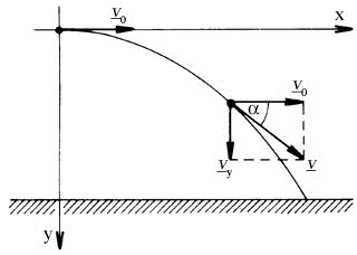
Ahogy a sebesség- és erővektorokkal megismerkednek a diákok, szinte azonnal szembetalálkoznak a vektorok összeadásának szabályával is. Kezdetben a párhuzamos vektorok összeadását ismerik meg, de hamarosan érzékeltetjük a (jellemzően a merőleges) szöget bezáró vektorok összeadására vonatkozó szabályt. Tipikus feladat erre a következő:
Egy folyó sebessége teljes szélességében ![]() m
m![]() s nagyságúnak tekinthető. Egy úszó a partra merőleges irányban
s nagyságúnak tekinthető. Egy úszó a partra merőleges irányban ![]() m
m![]() s-os sebességgel úszik át rajta.
s-os sebességgel úszik át rajta.
| a) Hol fog a túloldalon partot érni, ha a folyó 60 m széles? |
| b) Szerkesszük meg milyen irányban kell az úszónak úsznia, hogy a legrövidebb úton átjusson a túlsó partra? |
A megoldást az alábbi ábra szemlélteti.
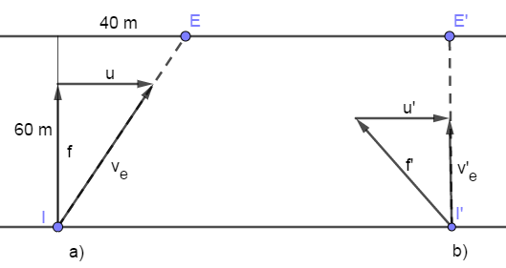
Ebben a feladatban a diákok alkalmazzák a vektorok összeadásának szabályát (olykor már általános iskolában is). Középiskolában viszont kilencedik osztály őszén meg is fogalmazzuk a paralelogramma-szabályt.
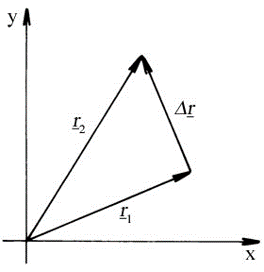 Tanév elején a vonatkoztatási rendszerekben a mozgások leírása a vonatkoztatási pontból kiinduló vektorokkal történik. Ekkor találkozik a diák először a helyvektor fogalmával. Az elmozdulásvektort a mozgás kezdő és végpontjába mutató helyvektorok különbségeként határozzuk meg, így a vektorok különbségének definiálása legkésőbb kilencedik osztály elején megtörténik.
Tanév elején a vonatkoztatási rendszerekben a mozgások leírása a vonatkoztatási pontból kiinduló vektorokkal történik. Ekkor találkozik a diák először a helyvektor fogalmával. Az elmozdulásvektort a mozgás kezdő és végpontjába mutató helyvektorok különbségeként határozzuk meg, így a vektorok különbségének definiálása legkésőbb kilencedik osztály elején megtörténik.
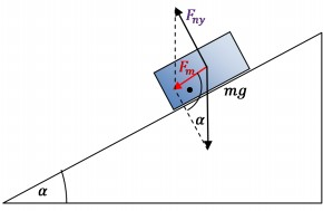
Az összetett mozgások vizsgálata során a vektorokat egymásra merőleges komponensekre bontjuk. Ezt gyakorolják a tanulók a hajítások esetén, amikor a sebességvektort vízszintes és függőleges komponensekre kell bontaniuk. A lejtőn lecsúszó test mozgását vizsgálva viszont lejtővel párhuzamos és lejtőre merőleges komponensekre bontjuk az erővektort.
A munkát az erő- és elmozdulásvektor skaláris szorzataként határozzuk meg, amit a tanulók tizenegyedik osztályban tanulnak matematikából. Fizikából a fogalmat 7. osztályban kezdjük el kialakítani, majd kilencedik osztályban pontosítjuk, végül tizenegyedik osztályban fakultáción mondjuk ki a fenti formában. A következő feladat azt mutatja be, hogy milyen lépéseken keresztül zajlik ez a folyamat.
Mekkora munkát végez a 80 N nagyságú erő a testen, ha a munkavégzés során az elmozdulás 300 m és az elmozdulás
| a) az erővel megegyező irányú, |
| b) merőleges az erőre, |
| c) 60 fokos szöget zár be az erővel? |
Megoldás:
a) Hetedik osztályban még csak abban az esetben számolunk munkát, amikor az erőhatás irányában történik az elmozdulás. Ilyenkor egyszerűen az erő és elmozdulás nagyságának szorzatával számolhatunk:
b) Kilencedik osztályban már komolyabban foglalkozunk az erő merőleges összetevőkre bontásával. A munka definícióját ekkor úgy pontosítjuk, hogy az erő és az erő irányú elmozdulás szorzataként számolható ki. Az elmozdulást felbontjuk erőirányú és arra merőleges összetevőkre. Ebben a feladatban az erő irányában nem történik elmozdulás, csak arra merőlegesen, így munkavégzés nem történik. A munkáról alkotott kép tehát kiegészül azzal, hogy az elmozdulásra merőleges erő nem végez munkát a testen.
c) Tizenegyedik osztályban fakultáción a szögfüggvények ismeretében ki tudjuk számolni az elmozdulásvektor erő irányú összetevőjének hosszát az ![]() képlettel, ha
képlettel, ha ![]() az erő és az elmozdulás által bezárt szög. Így a munkát a következőképpen számoljuk:
az erő és az elmozdulás által bezárt szög. Így a munkát a következőképpen számoljuk:
Matematika tanulmányainkat felhasználva ekkor már kimondhatjuk, hogy a munka az erő és az elmozdulás skaláris szorzataként számolható. A feladatban szereplő adatokkal:
Látható, hogy párhuzamos egyirányú vektorokra ez a képlet visszaadja a hetedikben tanultakat, merőleges elhelyezkedés esetén pedig nincs munkavégzés, hiszen ![]() . Ez a feladat is rávilágít arra, hogy mennyire fontos az erő felbontása az elmozdulásra merőleges és azzal párhuzamos összetevőkre. (Az mindegy, hogy az erőt bontjuk fel összetevőkre, vagy az elmozdulást.)
. Ez a feladat is rávilágít arra, hogy mennyire fontos az erő felbontása az elmozdulásra merőleges és azzal párhuzamos összetevőkre. (Az mindegy, hogy az erőt bontjuk fel összetevőkre, vagy az elmozdulást.)
A tizedikes fizikaórákon a vektorok vektoriális szorzásának előkészítése is megtörténik. Annak ellenére, hogy matematikából ez nem tananyag, érdemes erről tudnunk, így tudunk válaszolni azokra a kérdésekre, hogy a függvénytáblázatban a fizikai képletekben miért jelölik kétféleképpen a szorzást (![]() és
és ![]() jelekkel) és miért kell a skaláris jelző a skaláris szorzathoz, miért nem beszélhetünk egyszerűen csak szorzásról.
jelekkel) és miért kell a skaláris jelző a skaláris szorzathoz, miért nem beszélhetünk egyszerűen csak szorzásról.
Ezekre a kérdésekre adott válaszban támaszkodjunk a fizikai előismeretekre. Vegyük a munka képletét: ![]() . Ebben a vektormennyiségeket vastagon szedve jelöljük. Látszik, hogy két vektor szorzata nem vektor eredményre vezet. Nézzük meg, milyen jelenségkörben találkozhatnak a diákok olyan vektorszorzással, aminek eredménye is vektor!
. Ebben a vektormennyiségeket vastagon szedve jelöljük. Látszik, hogy két vektor szorzata nem vektor eredményre vezet. Nézzük meg, milyen jelenségkörben találkozhatnak a diákok olyan vektorszorzással, aminek eredménye is vektor!
Ha egy ![]() töltéssel rendelkező részecske a mágneses tér erősségét jellemző
töltéssel rendelkező részecske a mágneses tér erősségét jellemző ![]() mágneses indukcióvektorra merőlegesen
mágneses indukcióvektorra merőlegesen ![]() sebességgel mozog, akkor a töltött részecskére erő hat, aminek nagysága:
sebességgel mozog, akkor a töltött részecskére erő hat, aminek nagysága:
Az erő iránya merőleges a ![]() és
és ![]() vektorra, irányát „jobbkézszabállyal” határozzuk meg.
vektorra, irányát „jobbkézszabállyal” határozzuk meg.
Ha a részecske az indukcióvonalakkal párhuzamosan mozog, akkor nincs erőhatás. Általános esetben célszerű a sebességvektort az indukcióvonalakra merőleges és azzal párhuzamos összetevőkre bontani, amivel az erő nagyságára az
összefüggést kapjuk, ahol ![]() a
a ![]() és
és ![]() vektorok által bezárt szög. Ha az erő irányát a „jobbkézszabálynak” megfelelően meghatározzuk, már a vektoriális szorzat fogalmánál tartunk. Emelt szintű fizika csoportban ezt meg is mondhatjuk és megmutathatjuk, hogy a függvénytáblázatban szereplő
vektorok által bezárt szög. Ha az erő irányát a „jobbkézszabálynak” megfelelően meghatározzuk, már a vektoriális szorzat fogalmánál tartunk. Emelt szintű fizika csoportban ezt meg is mondhatjuk és megmutathatjuk, hogy a függvénytáblázatban szereplő
képlet ezt jelenti, amiben a ![]() jel a vektoriális szorzat jele.
jel a vektoriális szorzat jele.
Látjuk, hogy itt két vektor szorzása vektort eredményez. Emiatt tehát szükség van a kétféle jelölésre és a megkülönböztető skaláris (és itt elmondhatjuk, hogy vektoriális) jelzőre.
Ismétlés, elmélyítés, komplex gondolkodás fejlesztése
A fizikaórák jó színterei a tanult matematikai összefüggések gyakorlásának, elmélyítésének. Az órák zömében a diáknak rutinosan kell kezelnie a mértékegységek átváltását, a hatványozás azonosságait, a törtekkel való műveleteket, az egyenletrendezési lépéseket. A bevezetőben a teljesség igénye nélkül felsoroltam néhány területet, amelyek ismeretére szükségünk lehet a különböző fizikai problémák megoldásakor. Sok esetben a matematikaórán előforduló példáknál összetettebb feladatokban kell összekapcsolni az ezekről tanultakat. Egy közép- és egy emelt szintű fizika érettségi példán keresztül bemutatom, hogy milyen feladatokkal kell megbirkózniuk a diákoknak.
Egy gömb alakú, gömbszimmetrikus anyageloszlású, 9000 km sugarú bolygó körül két űrszonda kering körpályán. Az egyik szonda sebessége ![]() m
m![]() s, a pályájának sugara
s, a pályájának sugara ![]() km. A másik szonda pályájának sugara
km. A másik szonda pályájának sugara ![]() km. Mekkora a bolygó átlagsűrűsége? A gravitációs állandó:
km. Mekkora a bolygó átlagsűrűsége? A gravitációs állandó: 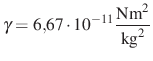 .
.
Megoldás:
A körpályán keringő űrszonda mozgásához szükséges centripetális erőt a Föld és a szonda között fellépő gravitációs erő biztosítja, így az 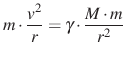 képlettel számolhatunk, ahol:
képlettel számolhatunk, ahol:
| a bolygó tömege: |
| az űrszonda tömege: |
| az űrszonda sebessége: |
| a körpálya sugara: |
| a bolygó sugara: |
A sűrűség kiszámításához először számoljuk ki a bolygó tömegét!
Az egyenletet egyszerűsítve és rendezve, illetve felhasználva hogy ![]() N
N![]() kg
kg![]() , azt kapjuk, hogy:
, azt kapjuk, hogy:
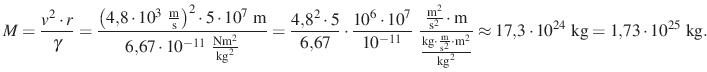
A bolygó átlagsűrűsége:
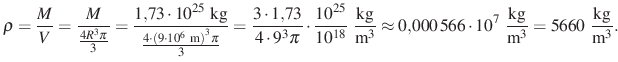
A feladat megoldásánál alkalmazott matematikai ismeretek: mértékegység-átváltás (fordított arányosság), normálalak, műveletek normálalakban megadott számokkal, műveletek törtekkel, hatványozás azonosságai, gömb térfogata, egyenletrendezés lépései, kerekítés. A diákok számára a feladatmegoldást nehezíti, hogy a tanult azonosságokat számok mellett a mértékegységekre is kell alkalmazni. Olykor könnyítésként az SI egységekben megadott mértékegységeket nem írjuk be az egyenletbe, csak megállapítjuk, hogy a végeredményt milyen egységben kapjuk.
A rendszeresen használt matematikai összefüggések (hatványozás, törtek, arányosság) mellett szinte minden ismeretre mutathatunk gyakorlati alkalmazást a fizika területéről. Ezek ismerete segítheti a tanulókat az emelt szintű érettségire készülésben, és elkerülhetjük vele azokat a kérdéseket, hogy „Mire fogom én ezt használni?” Természetesen ehhez szükséges, hogy az alkalmazási lehetőségekkel a matematikatanár is tisztában legyen és ha lehet, minél többel találkozzon a diák a matematikaórákon.
A második példa az emelt szintű fizika érettségi szóbeli részének egy mérési feladatából származik.
Különböző magasságokból leeső acélgolyó esési idejének mérésével határozza meg a nehézségi gyorsulás értékét!
Elméleti háttér: A szabadesést leíró ![]() képlet alapján az
képlet alapján az ![]() egyenesen arányos
egyenesen arányos ![]() -tel, így az
-tel, így az ![]() függvény meredekségének kétszerese adja
függvény meredekségének kétszerese adja ![]() értékét.
értékét.
| |
||||||
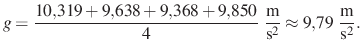
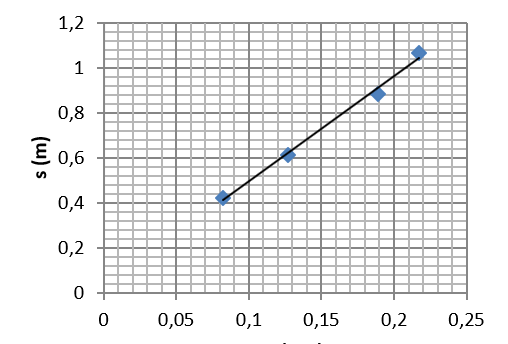
t2 (s2)
A megoldást egy konkrétan elvégzett mérés adatai alapján adtam meg kétféle módon. Az első módszerben a különböző esési magasságokhoz mért időadatok átlagolása után az első és hatodik oszlop adataiból a 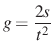 képletbe való behelyettesítéssel minden magasság mellett számoltunk egy
képletbe való behelyettesítéssel minden magasság mellett számoltunk egy ![]() értéket, majd ezeket átlagoltuk.
értéket, majd ezeket átlagoltuk.
A második módszerben a táblázat 1. és 6. oszlopa alapján ábrázoltuk az ![]() függvényt. A vízszintes tengelyen a
függvényt. A vízszintes tengelyen a ![]() értékeket ábrázolva a négyzetes úttörvényt mutatná a grafikonunk, így viszont egyenes arányosságot fedezhetünk fel a tengelyeken jelölt mennyiségek között. Ez jól látszik abból, hogy a mérési adatokra illesztett egyenes meghosszabbítása átmegy az origón.
értékeket ábrázolva a négyzetes úttörvényt mutatná a grafikonunk, így viszont egyenes arányosságot fedezhetünk fel a tengelyeken jelölt mennyiségek között. Ez jól látszik abból, hogy a mérési adatokra illesztett egyenes meghosszabbítása átmegy az origón.
A ![]() értékét a grafikon meredekségének kétszerese adja, ami a pontokra illesztett egyenes alapján:
értékét a grafikon meredekségének kétszerese adja, ami a pontokra illesztett egyenes alapján:
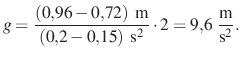
(A két érték közötti eltérés legfőbb oka, hogy a grafikon felbontása nem elég jó, a leolvasott értékek pontatlanok, de a módszer szemléltetésére alkalmasak.)
A fent ismertetett függvényábrázolási technikával matematikaórákon nem találkoznak a diákok. A technika azért hasznos, mert a pontokra parabolát szabad kézzel nem tudunk illeszteni, egyenes viszont egész könnyen illeszthető, amelynek a meredekségét is könnyen le tudjuk olvasni. Fizikaórán több állandó értékét határozhatjuk meg hasonló módon előállított lineáris függvény meredekségéből (például a rugóállandót a rugón függőlegesen rezgő test periódusidejének és a rezgő test tömegének kapcsolatát vizsgálva).
Mint láthattuk, a fizika feladatok megoldása általában összetett gondolkodást igényel. A fizikai ismeretek mellett a tanulónak a matematika több területén addig szeparáltan tanított ismereteit kell összekapcsolnia. Ezek a feladatok hozzájárulnak a komplex gondolkodás fejlesztéséhez, amire a matematika érettségi feladatok megoldásához is szükség lesz.
A bemutatott példákból látható, milyen fontos a számológép rutinos használata. Míg matematikaórán sok esetben törekszünk arra, hogy a tanuló fejben próbálja kiszámítani a végeredményt, addig fizikaórán már hetedik osztálytól tanítjuk a gyerekeket a számológép használatra. Ennek természetesen az az oka, hogy a mérésekből nyert adatok nem olyan kerek eredményekre vezetnek, mint amivel a matematikaórákon dolgoznak, így fejszámolásra kevésbé alkalmasak (mint az érettségi mérési feladatnál is láthattuk). A normálalak használatánál megbeszéljük, hogyan jelenik meg a számológép kijelzőjén, hogyan kell beírni a gépbe a hatványokat. Gyakoroljuk a műveleti sorrendnek megfelelően történő műveletsor beírását, a hatványokkal való számításokat, a szögfüggvények számítását, a fok és a radián közötti átváltást, stb. Ezek a gyakorlatok a matematikaórákon is nagyon hasznosnak bizonyulnak.
Egy-egy fizikafeladatot érdemes időnként matematikaórára, vagy szakkörre bevinni. Ezt tehetjük például úgy, hogy az aktuális matematikai problémát összekapcsoljuk az aktuális, vagy a már tanult fizikai problémával. Ennek előnye, hogy a tanulók szövegértése, a szakmai szövegben való eligazodása, komplex gondolkodása fejlődik. Emellett szakköröseink, versenyzőink a várhatóan emelt szintű matematika érettségijükre készülve konkrétan találkozhatnak különböző alkalmazási területekkel, miközben problémamegoldó képességük fejlődik.
Tantárgyunk tanítása során mindannyian hasonló problémákkal küzdünk. Az óraszám kevés, a tananyag sok és gyakran változik. Problémát okoz, hogy a diákok érdeklődését egyre nehezebb felkelteni, fenntartani. A széttagolt ismeretek integrálására nem marad idő. A problémák egy részére talán megoldást adhat a tantárgyak közötti összefonódások feltérképezése, és az ebből adódó lehetőség felismerése. A matematika és fizika között különösen sok kapcsolódási pont van. A cikk kereteibe ebből csak egy kis töredék fért bele. A Pázmány Péter Katolikus Egyetemen 2019. novemberében tartott előadásomhoz készített háttéranyag ennél jóval több lehetőségre is rámutat: https://tovabbkepzes.itk.ppke.hu/content/Matematika/2019/4_Fizika.pdf.
A cikkhez válogatott néhány példából talán kiderül, hogy érdemes belelátni ezekbe a kapcsolatokba. Fontos ismerni, hogy például a fizika tantárgy a matematikának milyen alkalmazási területeit mutatja be, mit és milyen életkorban használ fel a matematikai ismeretekből, továbbá milyen matematikai módszerekkel, fogásokkal ismerteti meg a tanulókat, amelyekkel a matematikaórákon nem találkoznak. Ennek ismeretében tanításunk színesíthető, időbeosztásunk hatékonyabbá tehető. A tantárgyi kapcsolódások ismeretében a nem matematikai irányban továbbtanuló diákjaink számára is rávilágíthatunk a tanított ismeretek fontosságára, alkalmazási lehetőségeire az élet különböző területein.
Kempelen Farkas Gimnázium, Budapest









