1. Bevezetés
A geometriai feladatok megoldása a komplex számsíkon sajátosan ötvözi mindazokat az előnyöket, amelyeket a vektoros, a trigonometriai és algebrai módszerek, illetve ezek egyidejű alkalmazásai szolgáltatnak. Oldja azt a geometriával szembeni – érzésem szerint egyre erősődő – fenntartást, amely a geometriára fordítható időkeret radikális csökkentésével kialakult tanulókban és tanárokban egyaránt. A bizonyítások tömörek, könnyen éthetőek. Az egész témának van egy belső eleganciája, harmóniája. Ez nagyon hamar magukkal ragadja a tehetséges gyerekeket. Tapasztalataim szerint a gyerekek nagyon megszeretik ezt a témakört.
Az alábbi tárgyalásból a csoport igényei, illetve a tanító tanár elképzelései szerint egyes részek el is hagyhatók, illetve mások részletesebben is tárgyalhatók.
2. Vektorok, geometriai transzformációk
Mindenképpen érdemes a tárgyalást ezzel a résszel kezdeni. Itt közvetlenül használhatók fel a komplex számokkal végzett műveletek tulajdonságai, az egységgyökök. A feladatok mindegyike megoldható tisztán geometriai módszerekkel vagy éppen hagyományosan vektorok forgatásával is. Ehhez a fejezethez tartozó feladatok rövid, diszkussziót nem igénylő, jól áttekinthető megoldásai már meg is mutatják a komplex számok használatának egyes előnyeit.
A legalapvetőbb módszereket egy ismert feladat két megoldásával mutatjuk be.
I. („vektoros”) megoldás.
Legyenek a háromszög csúcsai ![]() és
és ![]() . Az
. Az ![]() oldalra írt szabályos háromszög középpontja
oldalra írt szabályos háromszög középpontja ![]() , a
, a ![]() oldalra kifelé írt szabályos háromszög középpontja
oldalra kifelé írt szabályos háromszög középpontja ![]() , s végül a
, s végül a ![]() -ra írt szabályos háromszög középpontja
-ra írt szabályos háromszög középpontja ![]() pont. Legyen az
pont. Legyen az ![]() irányított szakasz az
irányított szakasz az ![]() ,
, ![]() a
a ![]() , s
, s ![]() irányított szakasz a
irányított szakasz a ![]() komplex szám. Jelentse továbbá
komplex szám. Jelentse továbbá ![]() az első hatodik egységgyököt. Ekkor a vektorok forgatásával - azaz a megfelelő komplex számok
az első hatodik egységgyököt. Ekkor a vektorok forgatásával - azaz a megfelelő komplex számok ![]() -nal történő szorzásával kapjuk, hogy
-nal történő szorzásával kapjuk, hogy ![]() ,
, ![]() ,
, ![]() .
.

Be kell látni, hogy ![]()
![]() -os elforgatottja
-os elforgatottja ![]() , vagyis
, vagyis
Ehhez felhasználjuk a következőket:
Egyrészt a hat komplex szám (vektor) összege nulla:
mivel ![]() , így
, így
Másrészt, mivel ![]() hatodik egységgyök
hatodik egységgyök ![]() , tehát
, tehát
Az ![]() nem nulla, emiatt
nem nulla, emiatt ![]() , illetve
, illetve ![]() .
.
Ezután a bizonyítandó egyenlőséget egy oldalra rendezve valóban látjuk, hogy
A másik bizonyítás a későbbi alkalmazásoknál (pl. Newton érintőnégyszögekre vonatkozó tételének bizonyítása) szintén jól használható.
II. („algebra és forgatás egyszerre”) megoldás.
Most kiszámoljuk először a ![]() és
és ![]() pontokhoz tartozó komplex számokat. A
pontokhoz tartozó komplex számokat. A ![]() komplex szám pozitív irányú
komplex szám pozitív irányú ![]() -os elforgatottja éppen
-os elforgatottja éppen ![]() . Ezt az
. Ezt az ![]() segítségével fel tudjuk írni:
segítségével fel tudjuk írni: ![]() . Ebből
. Ebből ![]() , és ezt követően ugyanígy
, és ezt követően ugyanígy ![]() és
és ![]() kifejezhetők:
kifejezhetők:
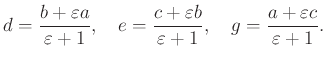
A ![]() háromszög szabályos, ha a
háromszög szabályos, ha a ![]() pont
pont ![]() körüli
körüli ![]() -os elforgatottja éppen az
-os elforgatottja éppen az ![]() pont, azaz
pont, azaz ![]() .
.

Ezzel a módszerrel sok esetben lehet dolgozni. A teljesség igénye nélkül: pl. Newton érintőnégyszögekre vonatkozó tétele, különféle Ceva-típusú kérdések, háromszögek és négyszögek oldalaira rajzolt háromszögek, négyzetek, szabályos sokszögek kérdései.
3. Körök és húrjaik
3.1. Húrok párhuzamossága
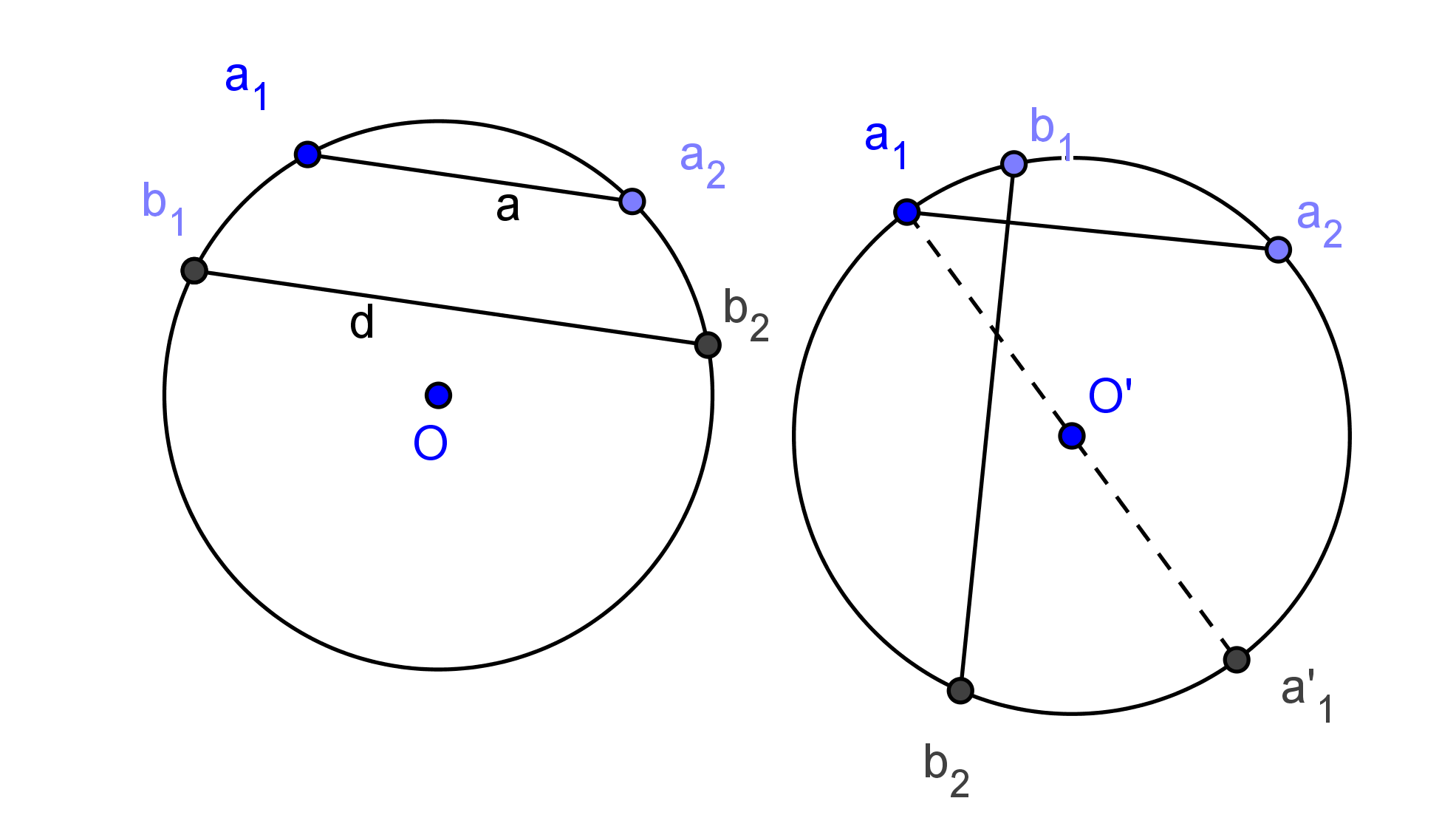
Az ![]() ív egyenlő az
ív egyenlő az ![]() ívvel, tehát
ívvel, tehát ![]() -et ugyanaz az
-et ugyanaz az ![]() középpontú forgatás viszi
középpontú forgatás viszi ![]() -be, amely
-be, amely ![]() -t
-t ![]() -be. A két komplex szám hányadosa ugyanaz az egységnyi hosszúságú komplex szám kell, hogy legyen.
-be. A két komplex szám hányadosa ugyanaz az egységnyi hosszúságú komplex szám kell, hogy legyen.
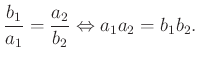
A bizonyítás oda-vissza olvasható, ez a párhuzamosság feltétele.
További fontos segédeszközökre is szükség van. Ezek bizonyítása megtalálható több, az irodalomjegyzékben felsorolt helyen is.
3.2. Kör húrjaival kapcsolatos segédeszközök
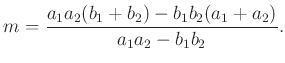
Ha a húrok merőlegesek, akkor ebből speciálisan:
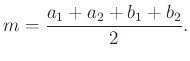
(Ugyanezt az eredményt kapjuk közvetlenül akkor is, ha ![]() szakasz és a
szakasz és a ![]() szakasz felezőpontjaiba mutató vektorok összegét vesszük. )
szakasz felezőpontjaiba mutató vektorok összegét vesszük. )
Két feladat megoldásával itt is ízelítőt adunk a megoldási lehetőségekről.
3.3. Háromszögre vonatkozó ismert feladat
Legyen a háromszög köréírt körének középpontja ismét az ![]() pont, a csúcsok
pont, a csúcsok ![]() és
és ![]() . A három helyvektor összege a magasságpontba mutat, tehát
. A három helyvektor összege a magasságpontba mutat, tehát
A magasságpont oldalakra vonatkozó tükörképei a körülírt körön vannak. Két ilyen pontot összekötő szakasz párhuzamos a talpponti háromszög oldalával. A magasságpont ![]() oldalra vonatkozó
oldalra vonatkozó ![]() tükörképét az
tükörképét az ![]() csúccsal összekötve a
csúccsal összekötve a ![]() és
és ![]() a kör egymásra merőleges húrjai, így
a kör egymásra merőleges húrjai, így 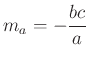 . Hasonlóan a magaságpont
. Hasonlóan a magaságpont ![]() -ra vonatkozó tükörképe
-ra vonatkozó tükörképe 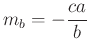 . Elegendő belátni, hogy az
. Elegendő belátni, hogy az ![]() és
és ![]() csúcsokhoz tartozó magasságoknak a körrel vett metszéspontjait összekötő húr merőleges a
csúcsokhoz tartozó magasságoknak a körrel vett metszéspontjait összekötő húr merőleges a ![]() és
és ![]() pontokat összekötő átmérőre. A merőlegesség feltételét újra felhasználva:
pontokat összekötő átmérőre. A merőlegesség feltételét újra felhasználva:
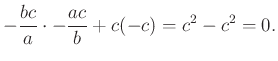
3.4. Húrnégyszög forgatása
Ismét ![]() középpontú körrel dolgozunk. A négyszög csúcsai
középpontú körrel dolgozunk. A négyszög csúcsai ![]() , a forgatást generáló egység-komplex szám
, a forgatást generáló egység-komplex szám ![]() . Ekkor pl.
. Ekkor pl. ![]() és
és ![]() elforgatottja
elforgatottja ![]() , illetve
, illetve ![]() . A két húr metszéspontja:
. A két húr metszéspontja:
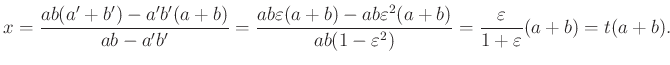
Rendre kapjuk, hogy ![]() és
és ![]() . Ebből
. Ebből ![]() , a négyszög paralelogramma.
, a négyszög paralelogramma.
3.5. További lehetőségek, feladatok
Minden olyan geometriai feladat esetében érdemes ezeket a módszereket is megfontolni, amikor egy körnek közvetítő szerepe van. Például:
- A háromszög magasságvonalai a talpponti háromszög szögfelezői
- Síkbeli egyeneshalmaz talpponti alakzata és metszéspontalakzata
- Simson-egyenes
- Adott körbe írt két egybevágó, azonos körüljárású háromszög megfelelő oldalainak metszéspontjai az eredetihez hasonló háromszöget határoznak meg
- Ennek a háromszögnek a magasságpontja a kör középpontja
- Brocard-féle pontok
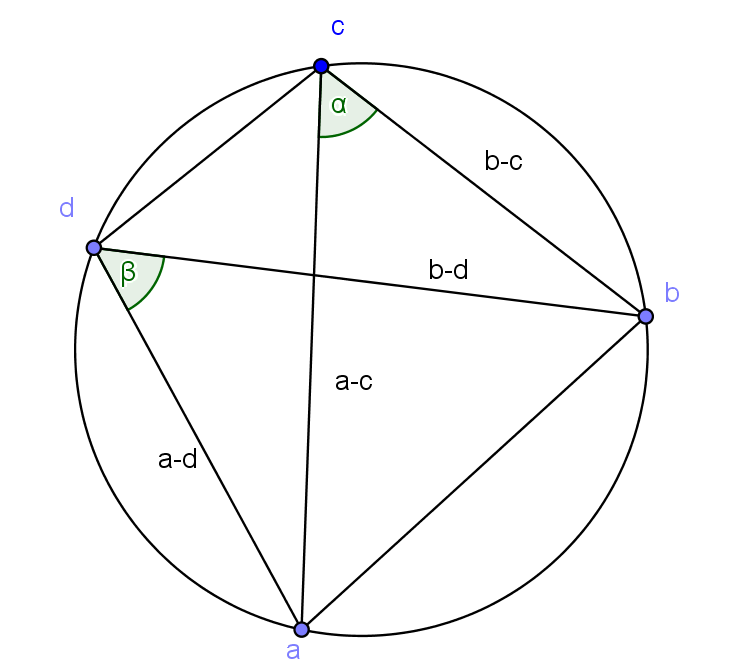
4. Köri pontnégyes – kettősviszony
Kicsit szűkebb tárgyalásnál ez a fejezet már el is hagyható. Speciális matematika osztályoknál azonban – véleményem szerint – érdemes ennek a tárgyalása, mert a vetítéseknél, a projektív geometria elemeinek tanulásánál is igen nagy hasznát vehetjük ezeknek az előzetes fogalmaknak,
4.1. Algebrai feltétel arra, hogy négy pont egy körön van
![]() , ezért
, ezért ![]() vektort ugyanolyan szögű forgatás viszi
vektort ugyanolyan szögű forgatás viszi ![]() -vel párhuzamos helyzetbe, mint
-vel párhuzamos helyzetbe, mint ![]() -t az
-t az ![]() -vel párhuzamos helyzetbe. Azaz van olyan
-vel párhuzamos helyzetbe. Azaz van olyan ![]() egységvektor, hogy
egységvektor, hogy ![]() és
és ![]() , ahol
, ahol ![]() és
és ![]() valós számok. Tehát
valós számok. Tehát
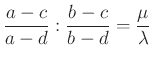
valós szám.
4.2. A kettősviszony
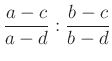 komplex számot, az
komplex számot, az Ha 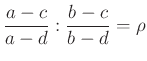 valós, akkor
valós, akkor 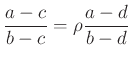 . Az
. Az ![]() és
és ![]() vektorok szöge vagy egyenlő az
vektorok szöge vagy egyenlő az ![]() és
és ![]() vektorok szögével, vagy azt
vektorok szögével, vagy azt ![]() -ra egészíti ki. Így
-ra egészíti ki. Így
A kettősviszonyra vonatkozó fenti tételnek a használatára remek lehetőséget kínál a háromszög Simson-egyenesére vonatkozó tétel tárgyalása.
4.3. Simson-egyenes

Bizonyítás: Legyenek az ![]() középpontú körön a háromszög csúcsai
középpontú körön a háromszög csúcsai ![]() , továbbá
, továbbá ![]() az a köri pont, ahonnan a merőlegeseket állítjuk. A
az a köri pont, ahonnan a merőlegeseket állítjuk. A ![]() -ből
-ből ![]() egyenesére állított merőleges a kört másodszor
egyenesére állított merőleges a kört másodszor ![]() pontban metszi. A két merőleges húr metszéspontja
pontban metszi. A két merőleges húr metszéspontja
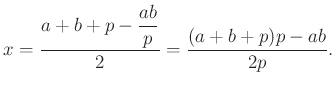
A másik két talppont:
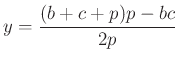 és
és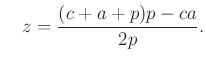
Az ![]() egy egyenesen vannak, ha
egy egyenesen vannak, ha 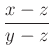 valós szám.
valós szám.
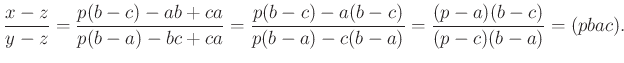
A ![]() köri pontnégyes kettősviszonya valós, tehát az
köri pontnégyes kettősviszonya valós, tehát az ![]() pontok valóban egy egyenesen vannak.
pontok valóban egy egyenesen vannak.
5. Trigonometriai alkalmazások
A nehezebb trigonometriai azonosságok bizonyításával gyakran nehézségek adódnak. A legtöbb bizonyítás nagyon egyedi ötletet, ügyes helyettesítést, és elsősorban a megfelelő sorrendben alkalmazott nevezetes trigonometriai azonosságok használatát követeli meg. Erre is kínálhatunk – sok esetben eredményesen használható – alternatív lehetőséget.
5.1. Trigonometriai számítás komplex számokkal
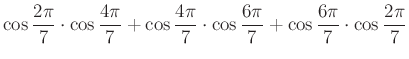 pontos értékét.
pontos értékét.
Legyen most ![]() az első hetedik egységgyök:
az első hetedik egységgyök:  , és emiatt
, és emiatt ![]() . Mivel az
. Mivel az ![]() egységnyi hosszúságú, ezért
egységnyi hosszúságú, ezért

Ebből már adódik is a sokszor használható formula:
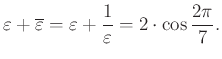
Ezt felhasználva a kiszámítandó kifejezés átírható:
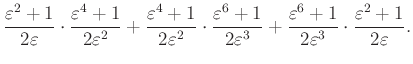
Közös nevezőre hozás után vegyük figyelembe, hogy ![]() , így
, így
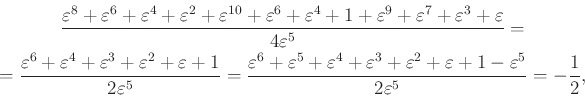 |
mivel ![]() és
és ![]() .
.
5.2. Szabályos sokszögre vonatkozó feladat
Feltehetjük, hogy a sokszög éppen az ![]() -edik egységgyökök szerint helyezkedik el és
-edik egységgyökök szerint helyezkedik el és ![]() . Tekintsük az
. Tekintsük az ![]() polinomot, amelynek gyökei pontosan az n-edik egységgyökök. A gyöktényezős alakban
polinomot, amelynek gyökei pontosan az n-edik egységgyökök. A gyöktényezős alakban ![]() az első egységgyök,
az első egységgyök,  :
:
Osszuk el mindkét oldalt ![]() -gyel:
-gyel:

Számoljuk ki kétféleképpen a ![]() -et:
-et:
másrészt a ![]() polinom n tagból áll:
polinom n tagból áll:
Mindkét oldal abszolút értékét véve a jobb oldali tényezők éppen a ![]() távolságok.
távolságok.
6. Néhány tétel bizonyítása
Ebben a fejezetben néhány olyan tételt mutatunk be, amelyek komplex számokkal is ragyogóan bizonyíthatóak. Egyes bizonyítások már a bevezető szakaszban, mások csak a kettősviszony tárgyalása után kerülhetnek sorra.
6.1. Heron-képlet
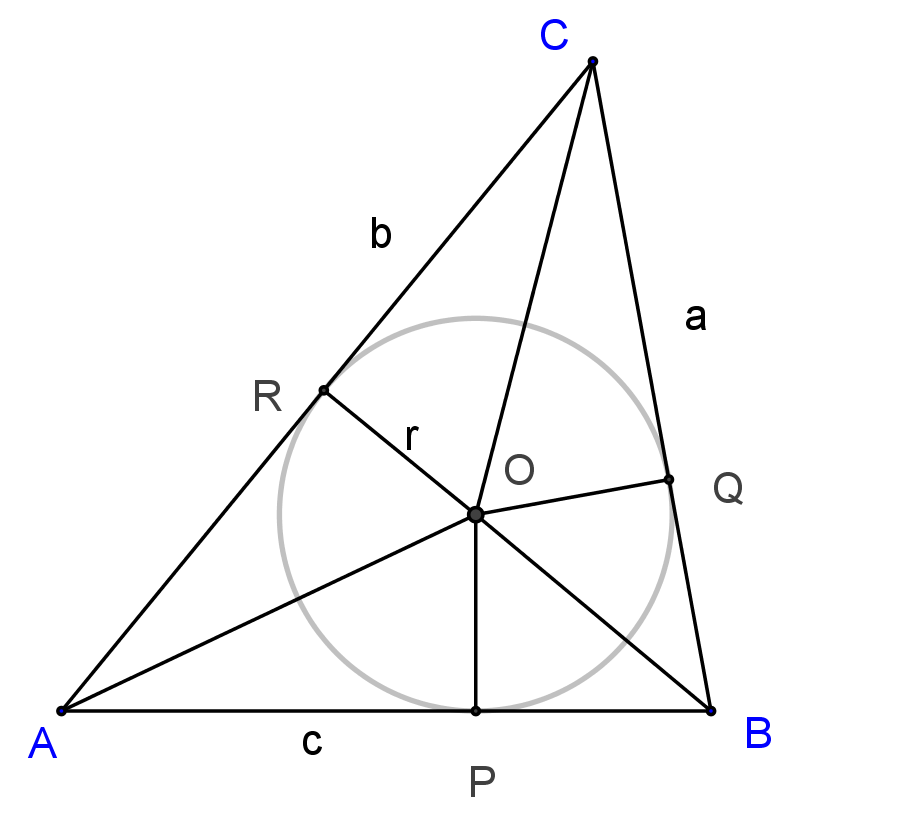
Az ábrán az ![]() pont a beírt kör középpontja,
pont a beírt kör középpontja, ![]() a beírt kör érintési pontjai,
a beírt kör érintési pontjai, ![]() a beírt kör sugara. Az oldalakat és szögeket a szokásos módon jelöljük. Ismert, hogy az érintőszakaszok
a beírt kör sugara. Az oldalakat és szögeket a szokásos módon jelöljük. Ismert, hogy az érintőszakaszok ![]() ,
, ![]() és
és ![]() .
.
Helyezzük el most az ![]() ,
, ![]() és
és ![]() háromszögeket úgy, hogy az
háromszögeket úgy, hogy az ![]() pont mindegyik háromszögre legyen a középpontban és a háromszögek
pont mindegyik háromszögre legyen a középpontban és a háromszögek ![]() hosszúságú befogója a valós tengelyre essen.
hosszúságú befogója a valós tengelyre essen.
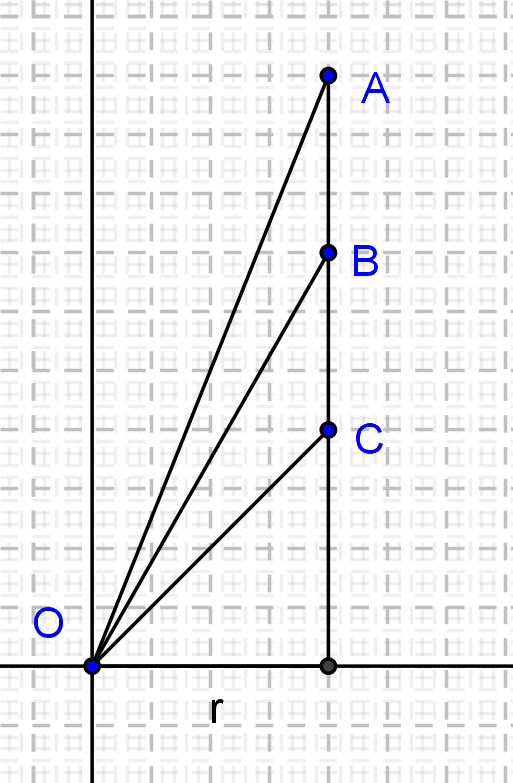
Így az ![]() csúcsoknak megfelelő komplex számok:
csúcsoknak megfelelő komplex számok:
A három komplex szám argumentumának összege 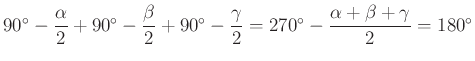 .
.
Szorzásakor az argumentumok összeadódnak, ennek megfelelően a három szám szorzatának képzetes része nulla kell, hogy legyen.
![\begin{equation*}\begin{aligned}A\cdot B \cdot C&=[r+(s-a)i][r+(s-b)i][r+(s-c)i]...
...[r^{2}(s-a)+r^{2}(s-b)+r^{2}(s-c)-(s-a)(s-b)(s-c)]. \end{aligned}\end{equation*}](/images/stories/latex/kissgezarlv/img141.png) |
A képzetes rész nulla:
Átrendezve és ![]() -sel szorozva
-sel szorozva
6.2. Ptolemaios-tétel
A műveletek elvégzése után a két oldal pontosan megegyezik. Ez egy algebrai azonosság.
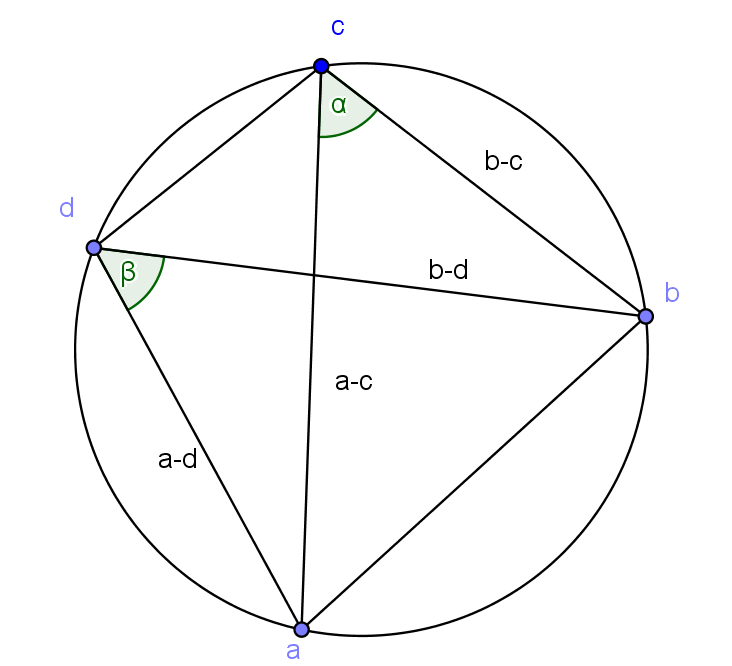
Bizonyítás: Legyen ![]() és
és ![]() . Osszuk végig az előző feladat azonosságát a
. Osszuk végig az előző feladat azonosságát a ![]() -vel.
-vel.
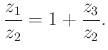
A 4. fejezet 4.1. és 4.2. eredményeit felhasználva, továbbá ismerve, hogy a törtek köri pontnégyesek kettősviszonyai, biztosan valósak, sőt a rajz szerint pozitív számok. A három vektor egyező irányú, így az összeg abszolút értéke egyenlő az összeadandók abszolút értékének összegével.
6.3. Newton érintőnégyszögekre vonatkozó tétele
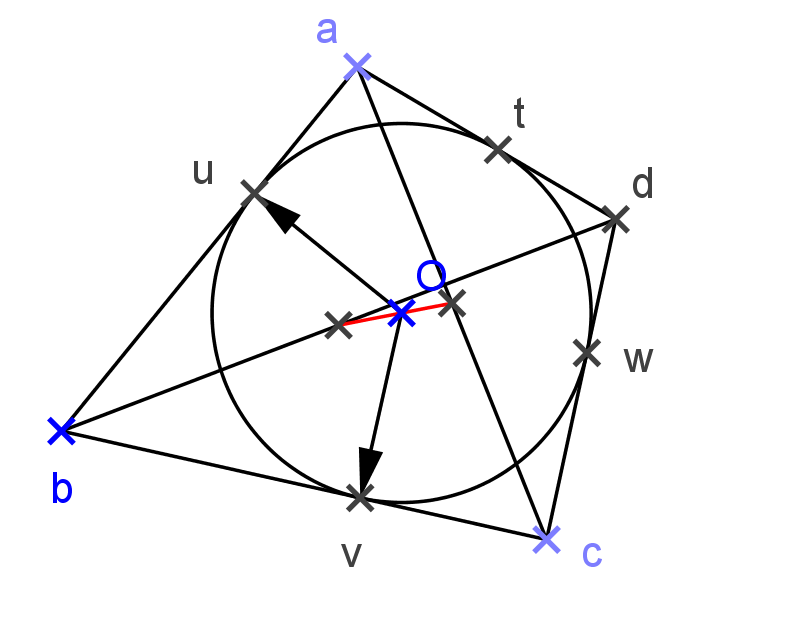
Bizonyítás: Válasszuk origónak a kör középpontját. Legyenek az oldalakon az érintési pontok rendre ![]() és
és ![]() . Fejezzük ki a csúcsokat az érintési pontok segítségével.
. Fejezzük ki a csúcsokat az érintési pontok segítségével. ![]() -os pozitív forgatással az
-os pozitív forgatással az ![]() elforgatottja párhuzamos lesz
elforgatottja párhuzamos lesz ![]() -val, a
-val, a ![]() elforgatottja pedig
elforgatottja pedig ![]() -vel. Tudjuk, hogy
-vel. Tudjuk, hogy ![]() , így az egyenletrendszerből:
, így az egyenletrendszerből: ![]() és
és ![]() ,
,
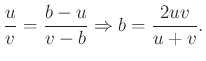
A többi csúcs ugyanígy: 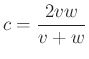 ,
, 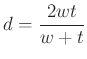 ,
, 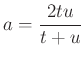 .
.
Be kell látni, hogy az átlók felezőpontjai, 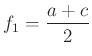 ,
,  és az origó egy egyenesen vannak. Az
és az origó egy egyenesen vannak. Az ![]() valós számszorosa
valós számszorosa ![]() -nek, arányuk valós.
-nek, arányuk valós.
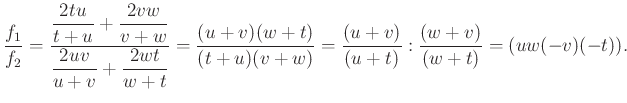
Ez a négy pont is egy körön van, hiszen ![]() és
és ![]() ,
, ![]() és
és ![]() átellenes köri pontok. A négy pont kettősviszonya valós.
átellenes köri pontok. A négy pont kettősviszonya valós.
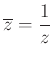 .
.
A bizonyítás befejező sora:
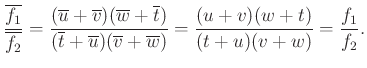
Tehát az arány valós.
7. Versenyfeladatok megoldása komplex számokkal
7.1. Kürschak József Tanulóverseny 2003/1.
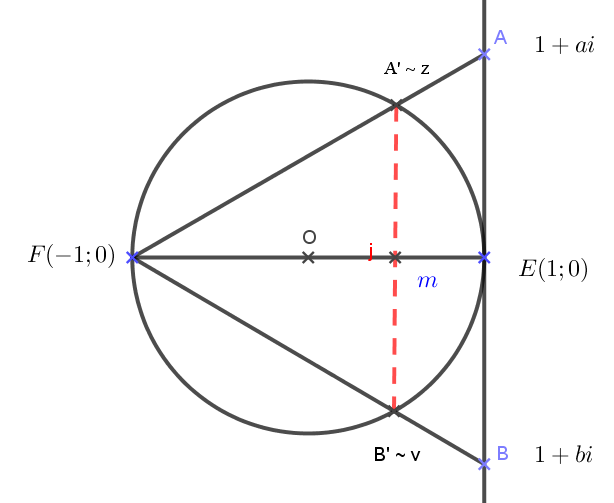
Legyen a kör egységnyi sugarú, középpontja az ![]() pont. Az ábra jelölései szerint az átmérő végpontjai:
pont. Az ábra jelölései szerint az átmérő végpontjai: ![]() pont az
pont az ![]() , az
, az ![]() pont pedig a
pont pedig a ![]() pont. Feleljen meg továbbá az
pont. Feleljen meg továbbá az ![]() pontnak az
pontnak az ![]() , a
, a ![]() pontnak az
pontnak az ![]() , az
, az ![]() -nek a
-nek a ![]() , és végül a
, és végül a ![]() -nek a
-nek a ![]() komplex szám. Számoljuk ki a
komplex szám. Számoljuk ki a ![]() komplex számot. Egyrészt
komplex számot. Egyrészt ![]() ,
, ![]() és
és ![]() egy egyenesen vannak,
egy egyenesen vannak,
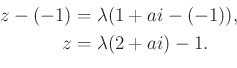 |
Másrészt tudjuk, hogy ![]() .
.
![$\displaystyle [\lambda(2+ai)-1][\lambda(2-ai)-1]=1 \Rightarrow \lambda=\dfrac{4}{4+a^2}.
$](/images/stories/latex/kissgezarlv/img190.png)
Ebből már ![]() számolható:
számolható:

A másik metszéspontra: 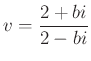 .
.
A ![]() négy köri pont. A
négy köri pont. A ![]() és
és ![]() húrok metszéspontja
húrok metszéspontja
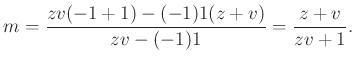
Behelyettesítés után
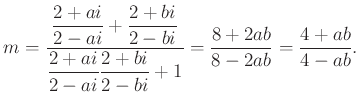
A feladat szövege szerint ![]() rögzített, így ez a pont nem függ az
rögzített, így ez a pont nem függ az ![]() és
és ![]() pontok választásától. Az
pontok választásától. Az ![]() és
és ![]() különböző előjelű valósak, így a nevező nem lesz nulla.
különböző előjelű valósak, így a nevező nem lesz nulla.
A feladat tárgyalását komplex számokkal, továbbá ezt a megoldást Szabó Kristóf 12. C. osztályos tanuló javasolta.
7.2. Arany Dániel Matematikai Tanulóverseny 2017/18. Haladók III. kategória 2. feladat
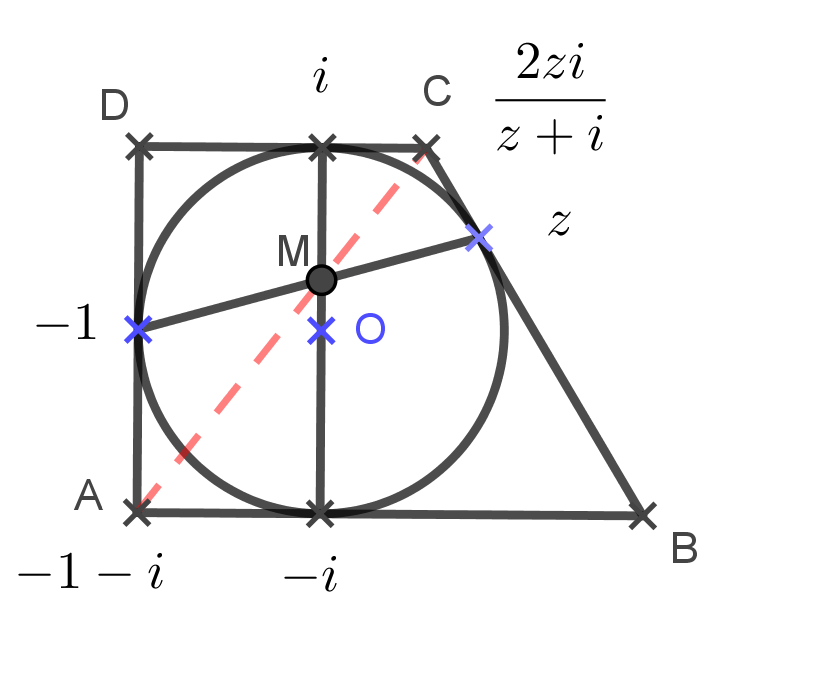
Legyen a trapézba írt kör középpontja ![]() , sugara
, sugara ![]() , alapjai párhuzamosak a valós tengellyel,
, alapjai párhuzamosak a valós tengellyel, ![]() szára párhuzamos a képzetes tengellyel. A kör érintési pontjai rendre
szára párhuzamos a képzetes tengellyel. A kör érintési pontjai rendre ![]() , az ábra szerint. A csúcsok:
, az ábra szerint. A csúcsok: 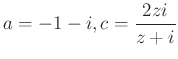 . A
. A ![]() pontot a Newton-tétel bizonyításánál megismert módszerrel írhatjuk fel az érintési pontok segítségével.
pontot a Newton-tétel bizonyításánál megismert módszerrel írhatjuk fel az érintési pontok segítségével.
![]() pont a kör húrjainak metszéspontja:
pont a kör húrjainak metszéspontja: 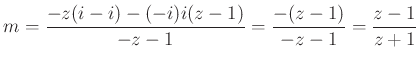 .
.
Számoljuk ki a ![]() szög tangensét:
szög tangensét:
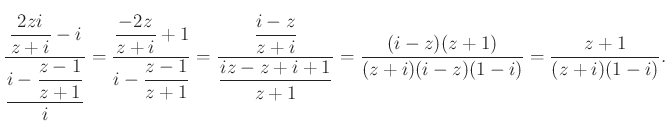
Végül a ![]() szög tangense:
szög tangense:

Az ![]() ,
, ![]() és
és ![]() pontok egy egyenesbe esnek.
pontok egy egyenesbe esnek.
7.3. Egy feladat a KöMaL-ból
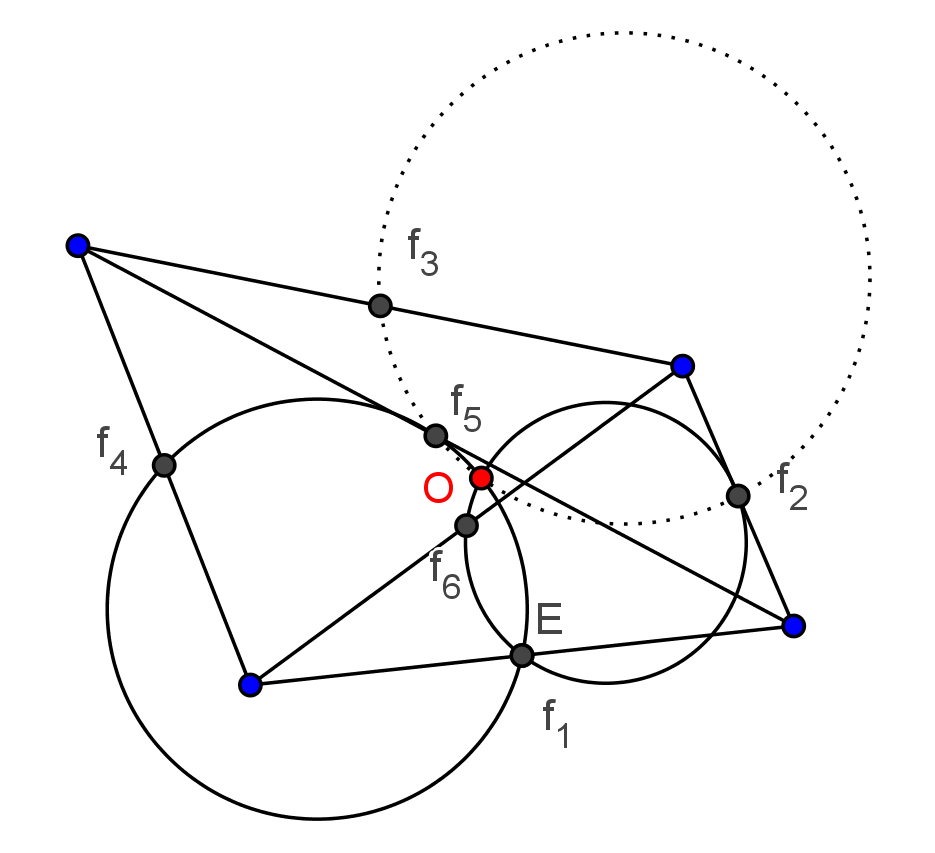
Legyenek a négyszög oldalainak és átlóinak felezőpontjai: ![]() . Az
. Az ![]() pontot úgy válasszuk meg, hogy az
pontot úgy válasszuk meg, hogy az ![]() , illetve az
, illetve az ![]() pontokon átmenő Feuerbach-körök az
pontokon átmenő Feuerbach-körök az ![]() -en kívül
-en kívül ![]() -ban messék egymást. (Az
-ban messék egymást. (Az ![]() egybe is eshet
egybe is eshet ![]() -gyel.) Elegendő azt megmutatni, hogy a két kör közös
-gyel.) Elegendő azt megmutatni, hogy a két kör közös ![]() metszéspontján pl. az
metszéspontján pl. az ![]() kör is átmegy. A bizonyítás az
kör is átmegy. A bizonyítás az ![]() körre hasonlóan menne.
körre hasonlóan menne.
Az ![]() kettősviszonyok valósak. Bizonyítandó, hogy az
kettősviszonyok valósak. Bizonyítandó, hogy az ![]() kettősviszony is valós. Tudjuk, hogy
kettősviszony is valós. Tudjuk, hogy

Szorozzuk össze a két egyenlőséget:
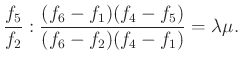
Tudjuk, hogy ![]() , mivel közös alapú háromszögek középvonal-vektorai, és ugyanilyen okból
, mivel közös alapú háromszögek középvonal-vektorai, és ugyanilyen okból ![]() , továbbá
, továbbá ![]() .
.
Ezeket behelyettesítve az egyszerűsítés után

ez éppen az ![]() .
.
8. További lehetőségek
8.1. Háromszögek hasonlósága
Az ![]() és
és ![]() azonos irányítású háromszögek akkor és csak akkor hasonlók, ha az
azonos irányítású háromszögek akkor és csak akkor hasonlók, ha az ![]() vektort ugyanaz a forgatva nyújtás viszi át az
vektort ugyanaz a forgatva nyújtás viszi át az ![]() –be, mint amelyik
–be, mint amelyik ![]() –t az
–t az ![]() –be. Ez azt jelenti, hogy van olyan f komplex szám, amellyel
–be. Ez azt jelenti, hogy van olyan f komplex szám, amellyel ![]() és
és ![]() . Ebből pedig
. Ebből pedig
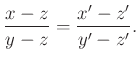
11. feladat.Az ![]() egy közös csúccsal rendelkező egyező körüljárású hasonló háromszögek, továbbá az
egy közös csúccsal rendelkező egyező körüljárású hasonló háromszögek, továbbá az ![]() csúcsok egy egyenesre illeszkednek. Mutassuk meg, hogy a
csúcsok egy egyenesre illeszkednek. Mutassuk meg, hogy a ![]() csúcsok is kollineárisak.
csúcsok is kollineárisak.
8.2. Szabályos háromszögre feltétel
Megoldás: Ha az ![]() háromszög szabályos, akkor egyben
háromszög szabályos, akkor egyben ![]() és
és ![]() háromszögek hasonlóak is. Használjuk az előző feltételt:
háromszögek hasonlóak is. Használjuk az előző feltételt:

Beszorzás és rendezés után
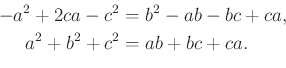 |
Mivel az átalakítások oda-vissza elvégezhetők és az ![]() háromszög akkor és csak akkor hasonló a
háromszög akkor és csak akkor hasonló a ![]() háromszöghöz, ha a háromszög szabályos, kaptunk egy „kényelmes” algebrai feltételt.
háromszöghöz, ha a háromszög szabályos, kaptunk egy „kényelmes” algebrai feltételt.
8.3. Szabályos háromszögre vonatkozó feladat
Megoldás: Legyen az eredeti háromszög ![]() , a négyzetközéppontok által meghatározott pedig
, a négyzetközéppontok által meghatározott pedig ![]() . Ha
. Ha ![]() az
az ![]() oldal fölé szerkesztett négyzet középpontja, akkor
oldal fölé szerkesztett négyzet középpontja, akkor ![]() merőleges
merőleges ![]() –re és vele egyenlő hosszúságú.
–re és vele egyenlő hosszúságú.
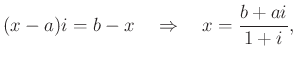
és ugyanígy: 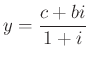 ,
, 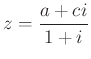 .
.
Annak feltétele, hogy ![]() szabályos legyen
szabályos legyen
Behelyettesítve és ![]() -nel beszorozva:
-nel beszorozva:
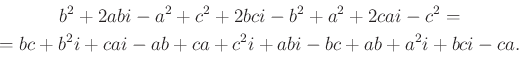 |
Rendezve és ![]() -vel egyszerűsítve pontosan:
-vel egyszerűsítve pontosan:
3. megjegyzés. Az ![]() háromszög szabályosságára ismert másik feltétel: ha
háromszög szabályosságára ismert másik feltétel: ha 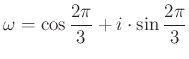 , az első harmadik egységgyök, a háromszög akkor és csak akkor pozitív körüljárású szabályos, ha
, az első harmadik egységgyök, a háromszög akkor és csak akkor pozitív körüljárású szabályos, ha ![]() .
.
8.4. Egyenes egyenlete a komplex számsíkon
Legyen egy egyenes normálvektora ![]() , adott pontja
, adott pontja ![]() . A
. A ![]() pont az egyenesen van, ha
pont az egyenesen van, ha ![]() .
.
Vegyük mindkét oldal konjugáltját, majd küszöböljük ki a ![]() -t.
-t.
 |
A ![]() valós szám, mert konjugáltak összege. Az egyenes egyenlete:
valós szám, mert konjugáltak összege. Az egyenes egyenlete: ![]() .
.
Megfordítva, ha ![]() és
és ![]() valós, akkor az
valós, akkor az ![]() normálvektorú és
normálvektorú és 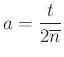 pontú egyenes egyenlete
pontú egyenes egyenlete
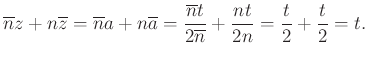
8.5. Kör egyenlete a komplex számsíkon
A ![]() középpontú
középpontú ![]() sugarú kör egyenlete:
sugarú kör egyenlete: ![]() , amit így írhatunk
, amit így írhatunk
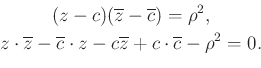 |
Jelöljük a ![]() valós számot
valós számot ![]() -sel. A kör egyenlete így:
-sel. A kör egyenlete így:
Megfordítva, ha ![]() , akkor a fenti alakú egyenlet mindig kör egyenlete, mert
, akkor a fenti alakú egyenlet mindig kör egyenlete, mert ![]() helyettesítéssel az egyenlet
helyettesítéssel az egyenlet ![]() alakra hozható. Ha
alakra hozható. Ha ![]() , akkor a kör átmegy az
, akkor a kör átmegy az ![]() ponton.
ponton.
8.6. Az egyenes és a kör közös egyenlete
Összefoglalva: az egyenes és a kör „közös” egyenlete
alakban adható meg.
Az egyenes esetében ![]() és
és ![]() .
.
A kör esetében a kör középpontja ![]() , sugara
, sugara 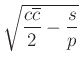 .
.
8.7. Az inverzió
Ha ![]() a komplex számsík nullpontja és az alapkör sugara 1, akkor az inverzió
a komplex számsík nullpontja és az alapkör sugara 1, akkor az inverzió
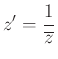
alakban adható meg. A ![]() és
és ![]() ugyanazon az
ugyanazon az ![]() -ból induló félegyenesen vannak: ha
-ból induló félegyenesen vannak: ha ![]() irányszöge
irányszöge ![]() , akkor
, akkor ![]() irányszöge
irányszöge ![]() és végül a
és végül a 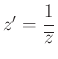 irányszöge ismét
irányszöge ismét ![]() . Milyen hatással van az inverzió a körre és az egyenesre? Induljunk ki a közös egyenletükből.
. Milyen hatással van az inverzió a körre és az egyenesre? Induljunk ki a közös egyenletükből.
Az inverz pontokra
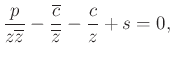
Beszorzás után:
Következtetések:
a) az ![]() -n átmenő egyenes (
-n átmenő egyenes (![]() ,
, ![]() ) képe önmaga;
) képe önmaga;
b) az ![]() -n átmenő kör (
-n átmenő kör (![]() ) képe az
) képe az ![]() -n át nem menő egyenes;
-n át nem menő egyenes;
c) az ![]() -n át nem menő egyenes (
-n át nem menő egyenes (![]() ,
, ![]() ) egyenes képe az
) egyenes képe az ![]() -n átmenő kör;
-n átmenő kör;
d) az ![]() -n át nem menő kör (
-n át nem menő kör (![]() ,
, ![]() ) inverze az
) inverze az ![]() -n át nem menő kör.
-n át nem menő kör.
Irodalomjegyzék
- [1] Reiman István: Geometria és határterületei, Szalay Könyvkiadó, (1999)
- [2] Reiman István: Geometriai feladatok megoldása a komplex számsíkon, Középiskolai szakköri füzet (1972)
- [3] I.M. Yaglom: Complex Numbers in Geometry, Academic Press, London, 1968, https://books.google.hu/books?id=LL_iBQAAQBAJ&pg=PR3&lpg=PR3&dq
- [4] Titu Andreescu–Dorin Andrica: Complex Numbers from A to ... Z, Birkhauser, 2006, https://books.google.hu/books?id=XZNCAAAAQBAJ&pg=PR4&dq
- [5] Fazekas M. Gimn. mat. munkaközösség: Matkönyv: Geometria 11.–12., Komplex számok a geomatriában fejezet, http://matek.fazekas.hu/
-
Megjegyzés
A 2018. évi Rátz László Vándorgyűlésen kértek fel a kollégák arra a megtisztelő feladatra hogy adjak egy vázlatos áttekintést arról, milyen fogalmakat és tételeket tanítok, milyen feladatokat dolgozok fel a komplex számok geomteriai alkalamazásairól a speciális matematika tagozaton. Ez a cikk ennek az előadásnak az anyagából született.









