Ha kell egy jó rajz, vagy már meglévő rajzon, képen, festményen szeretnénk dolgozni, érdemes megnyitni a GeoGebrát. Ha például egy metszéspont „leszalad” a képernyőről, elég átformázni, nem kell újrakezdeni. A rajzelemek, szerkesztési segédvonalak megjelenítését akár bemutató közben is szabályozhatjuk.
A GeoGebra azonban nem rajzoló, hanem dinamikus geometriai szerkesztő program, amely lehetővé teszi, hogy síkbeli és térbeli szerkesztéseket, bizonyításokat számítógépes környezetben, interaktív módon szemléltessünk, tanítsunk, tanuljunk.
A sokoldalúság alapja a dinamikus adatkezelés, amelynek során az alakzatokat logikai és (vagy) optikai szempontból definiálhatjuk, ami lehetővé teszi a rajz átformázását úgy, hogy az elemek közötti logikai kapcsolatok megmaradnak.
Ebben a cikkben a szerkesztés során létrehozott logikai rendszert ábrának, az alakzatok pillanatnyi optikai megjelenítését rajznak nevezzük. Ugyanannak az ábrának a felhasználásával sok-sok rajzot hozhatunk létre, megvizsgálhatjuk a speciális (a rajzra vonatkozó) és az (adott szerkesztési eljárás keretei között) általános tulajdonságok közötti viszonyt.
Egy alakzat logikai és optikai létezése közötti különbséget jól érzékelteti, hogy két egyenes rajzi megjelenítésekor „átfedés” is létrejöhet, amely csak a rajzon létezik, de az ábrához nem tartozik hozzá. Ugyanakkor az is előfordulhat, hogy például egy kör és egy egyenes metszéspontját definiáltuk, de a rajz pillanatnyi állapotában ez a metszéspont nem jön létre, mert valamelyik alakzatot nem metsző helyzetbe mozgattuk.
Mi most a térgeometriára koncentrálunk és olyan ötletekre hívjuk fel a figyelmet, amelyek hasznosak, de a programmal való első ismerkedéskor nem mindenki számára nyilvánvalóak.
A látvány beállításának hasznos eszköze a Jelölőnégyzet, amely ha ki van pipálva, akkor a logikai érték igaz, ha nincs kipipálva, akkor hamis. Jelölőnégyzetet a ![]() ikonra kattintva vagy a Parancsmezőbe beírva hozhatunk létre. Sajnos nem minden ablakban tudjuk engedélyezni az ikonját, ezért érdemes megismerni, hogy hogyan definiálhatjuk közvetlenül a parancsmezőben.
ikonra kattintva vagy a Parancsmezőbe beírva hozhatunk létre. Sajnos nem minden ablakban tudjuk engedélyezni az ikonját, ezért érdemes megismerni, hogy hogyan definiálhatjuk közvetlenül a parancsmezőben.
Gyakorló példa. Szerkesztettünk egy kockát, a kockába szabályos tetraédert és szabályos oktaédert írtunk. Meg szeretnénk mutatni, hogy a kocka lapközéppontjai és a tetraéder éleinek felezőpontjai ugyanannak a szabályos testnek, a szabályos oktaédernek a csúcsai. A látványt úgy akarjuk beállítani, hogy a kocka, a tetraéder és az oktaéder külön-külön és együtt is látható legyen, és hogy bemutatás közben is szabályozható legyen, hogy ezek közül éppen melyiket lehet látni.
A térbeli szerkesztéseket 3D-s nézetben célszerű végezni, amely a legördülő menüsorból (Nézet, 3D-s nézet) vagy a Ctrl + Shift + 3 billentyűkombinációval választható ki.
A kockát a Kocka parancsikon segítségével szerkeszthetjük:
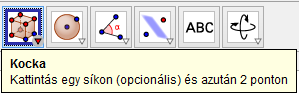
A kockába írt szabályos tetraédert is parancsikon segítségével szerkeszthetjük, például a Gúla parancsikont alkalmazva a kocka egy csúcsából induló három élének végpontjait választjuk alaplap csúcsainak, a belőle induló testátló másik végpontját pedig a gúla csúcsának.

A szabályos oktaéder csúcsait, azaz a kocka lapközéppontjait a Felezőpont parancsikon segítségével szerkesztjük. A szabályos oktaédert összerakhatjuk két olyan gúlából, amelyek alapnégyzete közös, így ehhez is a Gúla parancsikont használhatjuk.
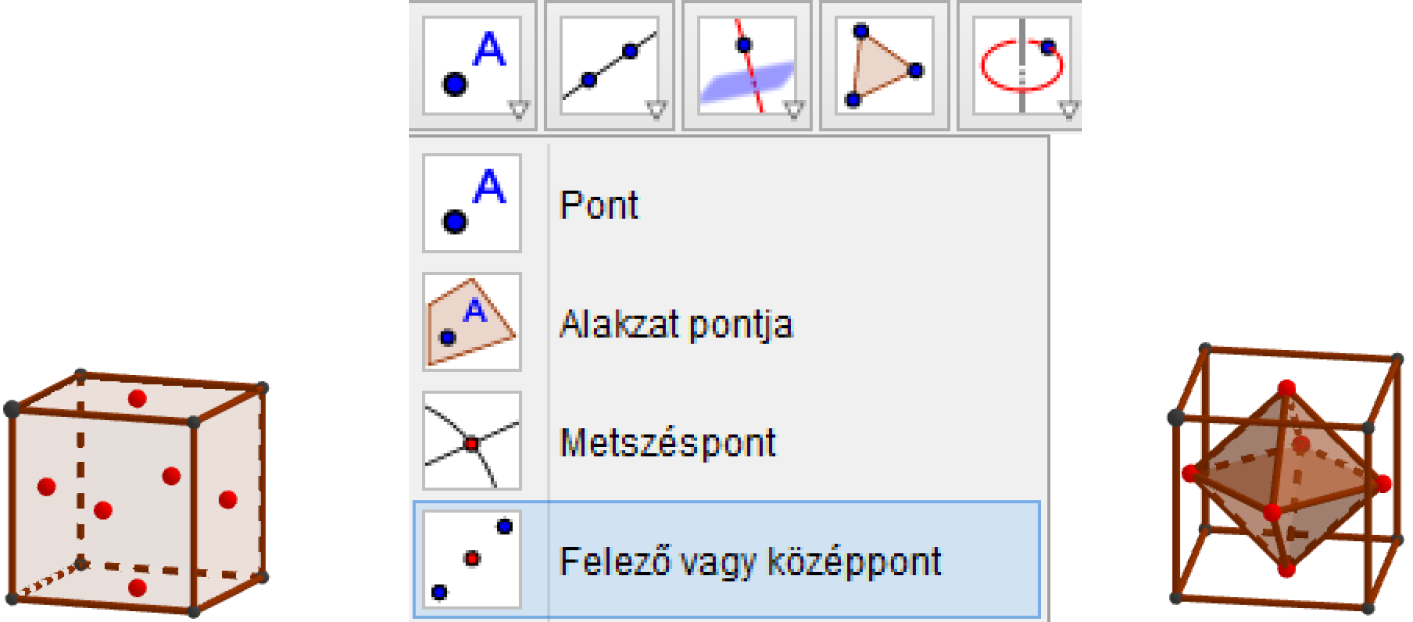
Ha a kocka láthatóságát Jelölőnégyzettel akarjuk szabályozni, akkor létrehozunk egy erre szolgáló jelölőnégyzetet, majd a logikai értéket összekötjük az alakzattal, hogy hatással legyen a látványra.
- A parancsmezőbe beírjuk, hogy Kocka = true. Az Enter leütése után az algebra ablakban a logikai értékek között megjelenik a Kocka = true elem, a 2D ablakban a Kocka felirat és a kipipált Jelölőnégyzet.

- A kocka tulajdonságai ablakban a haladó fülre kattintva beállítjuk a láthatóság feltételét:
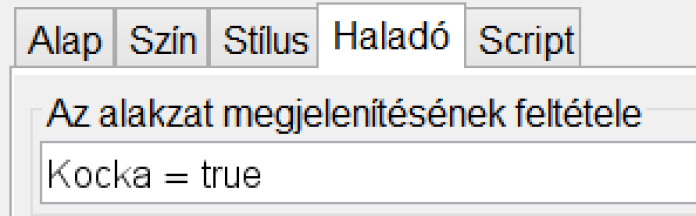
Hasonlóképpen jártunk el a tetraéder és az oktaéder esetében is (1. ábra). Mivel az oktaédert két gúlából raktuk össze, így mindkét gúla láthatóságát a megfelelő jelölőnégyzet kipipálásától tettük függővé. Ha elkészültünk a beállításokkal, akkor be is zárhatjuk az algebra ablakot. Vigyázzunk, a 2D ablakot (Rajzlap) ne zárjuk be, mert a Jelölőnégyzet csak ott jelenik meg!
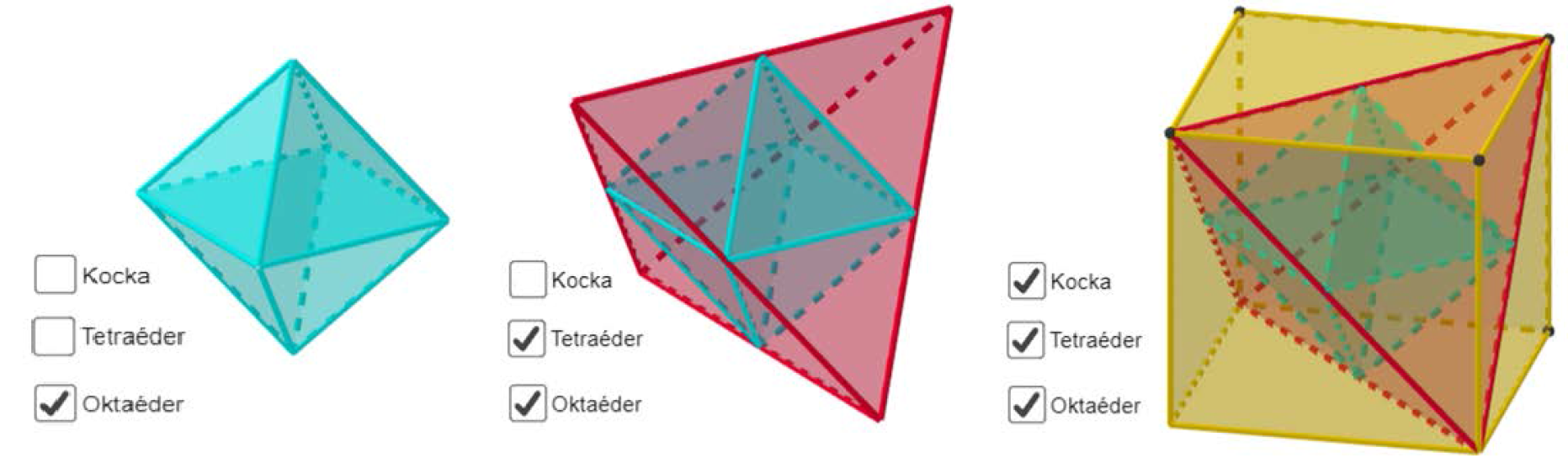
1. ábra: A kocka, a kockába írt szabályos tetraéder és a szabályos oktaéder láthatósága Jelölőnégyzettel szabályozva. (Vásárhelyi 2018b https://ggbm.at/gr292jkN)
Hasonló eredményt érhetünk el, ha nem Jelölőnégyzetet, hanem Csúszkát használunk.
A Csúszka is a 2D ablakban látszik, ezért függőlegesre állítottuk, hogy keskenyre vehessük a 2D ablakot. A mi példánkban egy olyan Csúszkát definiáltunk, amelynek az ![]() változója 0, 1, 2, és 3 értékeket vehet fel (2. ábra). A kocka láthatóságának feltétele
változója 0, 1, 2, és 3 értékeket vehet fel (2. ábra). A kocka láthatóságának feltétele ![]() , a tetraéderé
, a tetraéderé ![]() , az oktaéderé (a 2 gúláé)
, az oktaéderé (a 2 gúláé) ![]() . A jelölőnégyzetes megoldáshoz képest elvesztettük azt a lehetőséget, hogy együtt és külön-külön is láthatóak legyenek az egyes szabályos testek.
. A jelölőnégyzetes megoldáshoz képest elvesztettük azt a lehetőséget, hogy együtt és külön-külön is láthatóak legyenek az egyes szabályos testek.
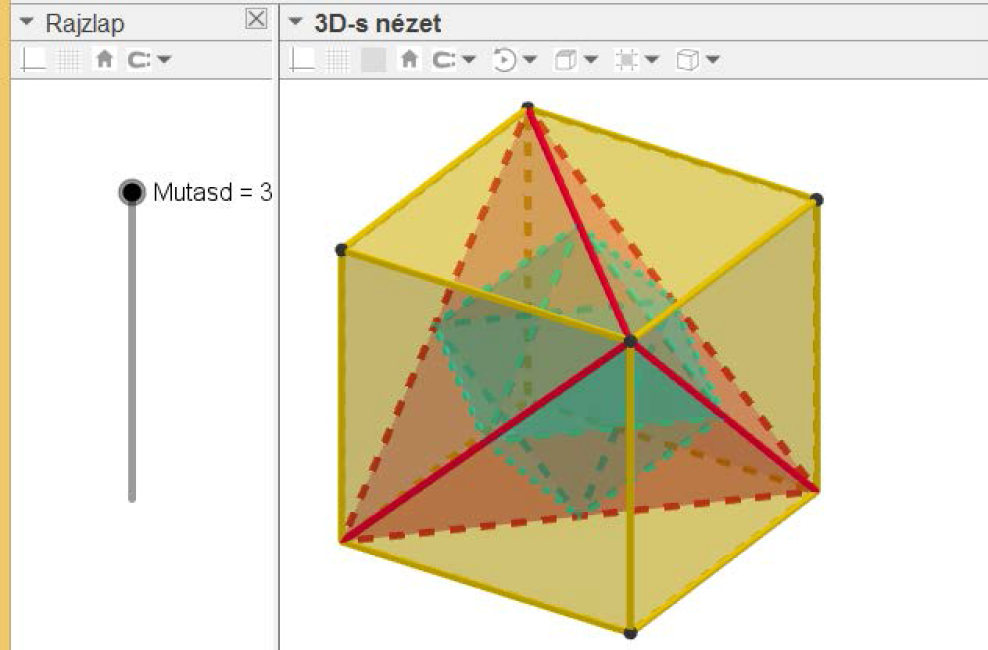
2. ábra: A kocka, a kockába írt szabályos tetraéder és a szabályos oktaéder láthatósága Csúszkával szabályozva. (Vásárhelyi 2018c https://ggbm.at/wTfsh8qV)
Bemutatáskor az alakzat forgatásához a 3D-s nézet forgatása ![]() ikont használjuk. Wertheimer (1912) kísérletei óta tudományosan is bizonyított, hogy a térélmény kialakulásában nagy szerepe van a megmozgatott, elfordított 3D-s nézetnek. A GeoGebrában 3D ábrákkal biztosítható a mozgásélmény. Az álló és a mozgó kép látványa közötti különbség minden szemlélőre komoly benyomást tesz. Olyanok számára is létrejön a térélmény, akik a statikus képen nem igazodnak el.
ikont használjuk. Wertheimer (1912) kísérletei óta tudományosan is bizonyított, hogy a térélmény kialakulásában nagy szerepe van a megmozgatott, elfordított 3D-s nézetnek. A GeoGebrában 3D ábrákkal biztosítható a mozgásélmény. Az álló és a mozgó kép látványa közötti különbség minden szemlélőre komoly benyomást tesz. Olyanok számára is létrejön a térélmény, akik a statikus képen nem igazodnak el.
A Jelölőnégyzet mind a tanári bemutató, mind a diákok önálló problémamegoldása során nagyon hasznos. A következő feladatban három különböző megoldást szemléltetünk ugyanazon az ábrán. Jelölőnégyzetek segítségével érjük el, hogy az egyes meggondolások ne zavarják egymást.
Feladat (Hajnal 1982): Egy négyoldalú szabályos gúlát kettévágunk egy olyan síkkal, amely átmegy az alaplap középpontján és párhuzamos az egyik oldallappal. Számítsuk ki a kapott részek térfogatának arányát!
Megszerkesztjük a négyoldalú szabályos gúlát. Szerkesztünk egy ![]() oldalú négyzetet, változtatható hosszúságúra állítjuk be az
oldalú négyzetet, változtatható hosszúságúra állítjuk be az ![]() magasságot és megszerkesztjük a négyoldalú szabályos gúlát (3. ábra). A gúla oldaléleinek hossza
magasságot és megszerkesztjük a négyoldalú szabályos gúlát (3. ábra). A gúla oldaléleinek hossza 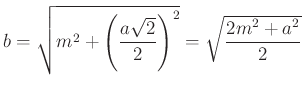 , oldallapjainak magassága
, oldallapjainak magassága 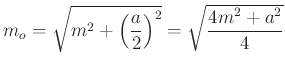 és a térfogata
és a térfogata 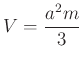 .
.
A dinamikus geometriai szemléltetés mellett szól, hogy a gúla magassága akármekkora lehet, amit kézzel fogható modellen nem tudunk szemléltetni.
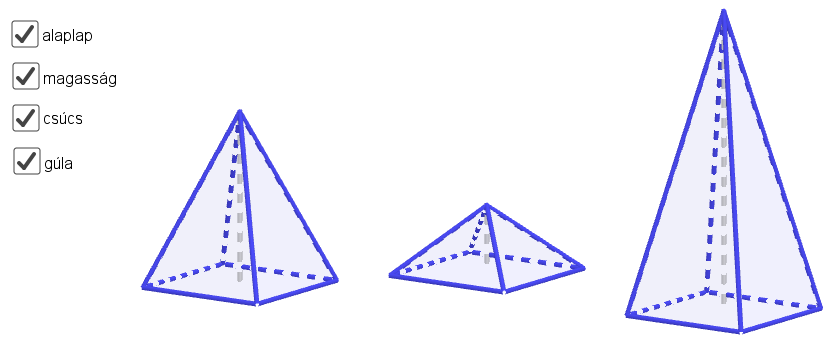
3. ábra: Négyoldalú szabályos gúla különböző magasságokkal. (Vásárhelyi 2018d https://ggbm.at/J9KmhzeA)
Megszerkesztünk egy, az alaplap középpontján áthaladó és az egyik oldallappal párhuzamos síkot. Ha magunknak szerkesztünk, ezt közvetlenül is megtehetjük a ![]() ikonra kattintva az oldallap és a középpont kiválasztásával. A tanulók számára tanulságosabb, ha a középponton át az oldallappal párhuzamos egyeneseket húznak.
ikonra kattintva az oldallap és a középpont kiválasztásával. A tanulók számára tanulságosabb, ha a középponton át az oldallappal párhuzamos egyeneseket húznak.
Megkeressük a gúlával alkotott metszetet, arra építve, hogy két párhuzamos sík egy harmadik síkot párhuzamos egyenesekben metsz. (Ezt az ismeretet tartalmazza a Segítség.)
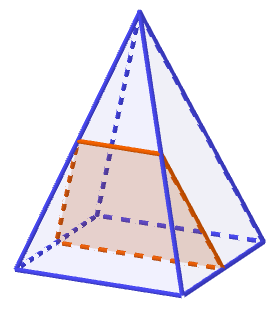
4. ábra: A síkmetszet egy húrtrapéz. (Vásárhelyi 2018d https://ggbm.at/J9KmhzeA)
Megállapítjuk, hogy húrtrapézt kaptunk (4. ábra). A húrtrapéz egyik alapja ![]() hosszúságú, a négyzet középvonala. Másik alapja
hosszúságú, a négyzet középvonala. Másik alapja ![]() hosszúságú, az egyik oldallapnak a négyzettel párhuzamos középvonala. A húrtrapéz szárai a metsző síkkal párhuzamos lap oldaléleivel párhuzamos középvonalak, ezért
hosszúságú, az egyik oldallapnak a négyzettel párhuzamos középvonala. A húrtrapéz szárai a metsző síkkal párhuzamos lap oldaléleivel párhuzamos középvonalak, ezért 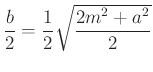 hosszúságúak.
hosszúságúak.
A sík a gúlából egy olyan testet vág le, amelynek lapjai (5a ábra)
- egy téglalap, amelynek oldalai
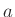 és
és 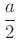 hosszúságúak;
hosszúságúak; - két egybevágó egyenlő szárú háromszög, amelyek alapja
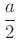 hosszúságú, száraik pedig
hosszúságú, száraik pedig 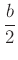 hosszúságúak;
hosszúságúak; - két egybevágó húrtrapéz, ezek egyik alapja
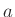 , másik alapja
, másik alapja 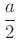 hosszúságú, a szárak hossza pedig
hosszúságú, a szárak hossza pedig 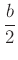 .
.
A levágott testnek van két szimmetriasíkja, ezek merőlegesek az alaptéglalapra és illeszkednek annak egy-egy középvonalára. Az egyik a gúlával közös szimmetriasík. (5b és 5c ábra)
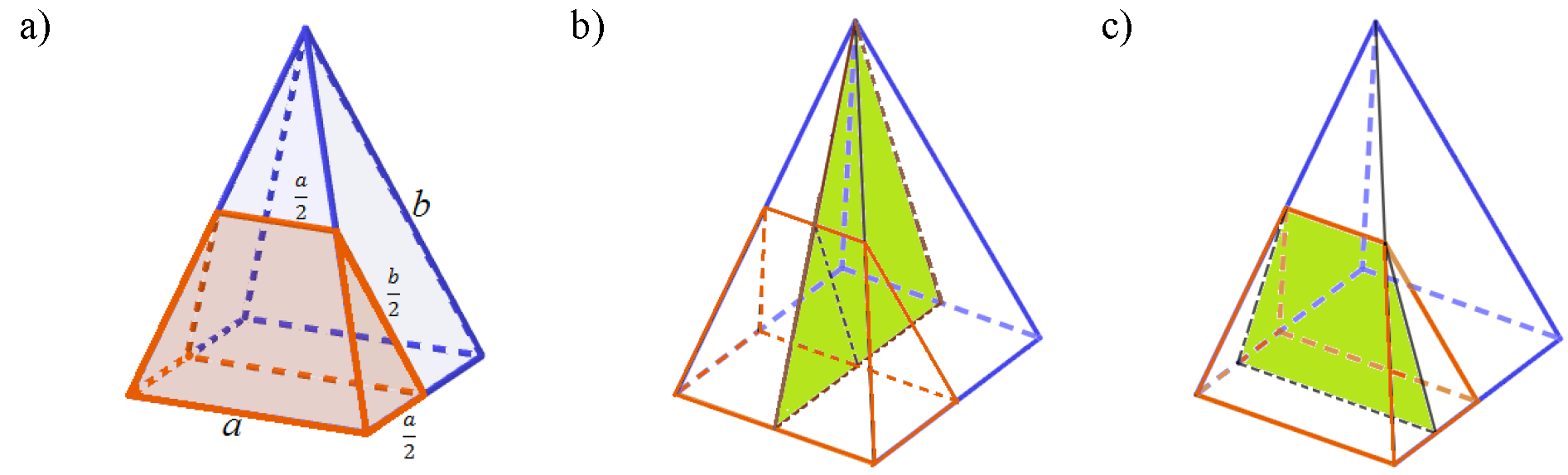
5. ábra: A levágott rész és szimmetriasíkjai.
A térfogat meghatározására mutatunk három meggondolást. Ezek közös gondolata, hogy részekre bontással, illetve átdarabolással olyan testeket alkotunk, amelyek térfogatát egyszerűbb meghatározni.
A felbontás szemléltetéséhez eltoljuk az egyes részeket. Ehhez összekötjük egy szakasszal a kiválasztott kiindulási és egy véghelyzetet, és egy olyan eltolásvektort használtunk, amelynek kezdőpontja a kiindulási pont, végpontja pedig elmozdulhat a kiindulási és véghelyzet közötti szakaszon.
1. Megoldás: Két kis gúlára és egy háromszög alapú egyenes hasábra bontjuk a levágott részt, majd a két kis gúlából összerakjuk az eredeti gúla ![]() arányban kicsinyített mását (6. ábra).
arányban kicsinyített mását (6. ábra).
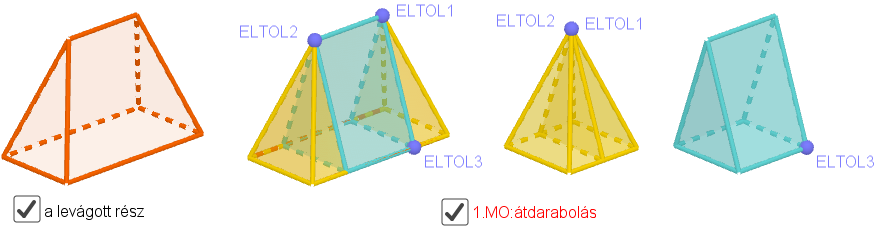
6. ábra: A levágott rész átdarabolása négyoldalú szabályos gúlává és egyenes hasábbá. (Vásárhelyi 2018d https://ggbm.at/J9KmhzeA)
A kicsinyített gúla térfogata az eredeti gúla térfogatának ![]() része, azaz
része, azaz 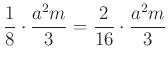 .
.
A hasáb háromszöglapjai egyenlő szárú háromszögek, amelyek alapja ![]() , magassága
, magassága ![]() , ezért a területük
, ezért a területük ![]() . A hasáb magassága
. A hasáb magassága ![]() , így a hasáb térfogata
, így a hasáb térfogata 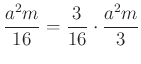 . A levágott rész térfogata tehát
. A levágott rész térfogata tehát 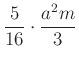 , ami az eredeti gúla térfogatának
, ami az eredeti gúla térfogatának ![]() része.
része.
A metsző sík olyan részekre bontja a gúlát, amelyek térfogatának aránya 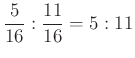 . Látható, hogy ez független a kiindulási gúla alapélének és magasságának hosszától.
. Látható, hogy ez független a kiindulási gúla alapélének és magasságának hosszától.
2. Megoldás: A levágott testet felosztjuk egy négyoldalú szabályos gúlára és egy háromszög alapú ferde hasábra. (7. ábra)
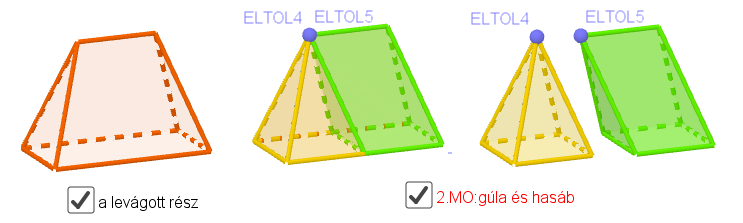
7. ábra: A levágott rész felosztása hasábra és gúlára. (Vásárhelyi 2018c https://ggbm.at/J9KmhzeA)
A kis gúla az eredeti gúla ![]() arányban kicsinyített mása. A ferde hasáb alapja egybevágó a kis gúla oldallapjaival, a magassága a két párhuzamos sík távolságával egyenlő. A ferde hasábot átdarabolhatjuk (az 1. megoldásban is szereplő) egyenes hasábbá, vagy közvetlenül meghatározhatjuk a ferde hasáb térfogatát.
arányban kicsinyített mása. A ferde hasáb alapja egybevágó a kis gúla oldallapjaival, a magassága a két párhuzamos sík távolságával egyenlő. A ferde hasábot átdarabolhatjuk (az 1. megoldásban is szereplő) egyenes hasábbá, vagy közvetlenül meghatározhatjuk a ferde hasáb térfogatát.
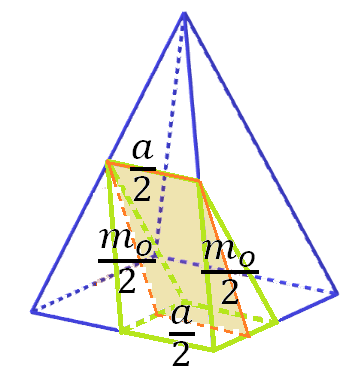
A ferde hasáb (és egyben a levágott rész) szimmetriasíkja egy paralelogrammában metszi a hasábot. A paralelogramma egyik párhuzamos oldalpárjának hossza az eredeti gúla alapélének fele ![]() . illetve oldallap magasságának fele
. illetve oldallap magasságának fele ![]() . A paralelogramma
. A paralelogramma ![]() oldalpárhoz tartozó magassága a gúla magasságának fele
oldalpárhoz tartozó magassága a gúla magasságának fele ![]() . A paralelogramma területe így
. A paralelogramma területe így 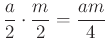 , amiből az
, amiből az ![]() oldalpárhoz tartozó magasság
oldalpárhoz tartozó magasság 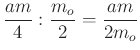 , ami egyben a hasáb magassága is.
, ami egyben a hasáb magassága is.
A hasáb alapja egyenlőszárú háromszög, amelynek alapja ![]() , magassága
, magassága ![]() , ezért a területe
, ezért a területe 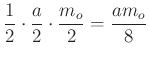 . A hasáb magassága
. A hasáb magassága ![]() , így a hasáb térfogata
, így a hasáb térfogata 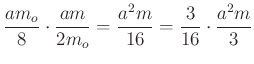 . A levágott rész térfogata a kicsinyített gúla és a hasáb térfogatának összege,
. A levágott rész térfogata a kicsinyített gúla és a hasáb térfogatának összege, 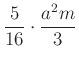 , ami az eredeti gúla térfogatának
, ami az eredeti gúla térfogatának ![]() része. A metsző sík az eredeti gúlát olyan részekre bontja, amelyek térfogatának aránya
része. A metsző sík az eredeti gúlát olyan részekre bontja, amelyek térfogatának aránya 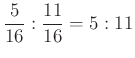 .
.
3. Megoldás: A levágott testet felosztjuk két egybevágó négyoldalú szabályos gúlára és egy tetraéderre. (8. ábra)
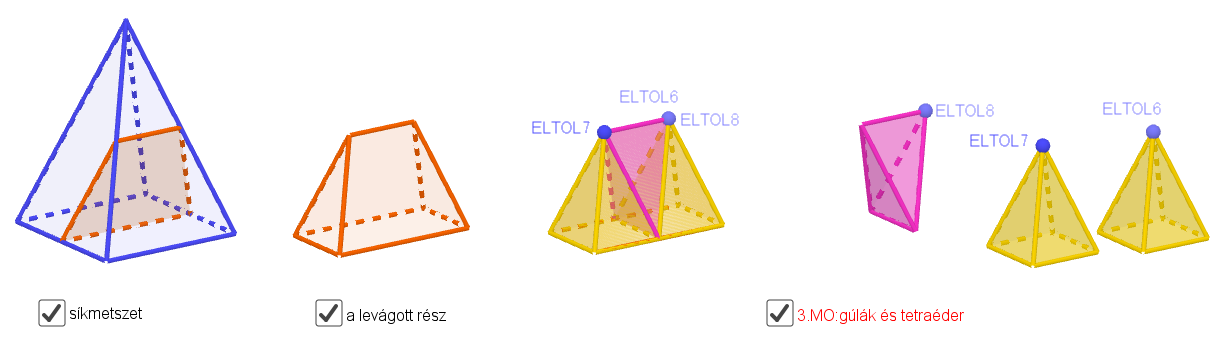
8. ábra: A levágott rész felosztása két gúlára és tetraéderre. (Vásárhelyi 2018c https://ggbm.at/J9KmhzeA)
A két gúla az eredetiből ![]() arányú kicsinyítéssel származik, együttes térfogatuk az eredeti gúla térfogatának
arányú kicsinyítéssel származik, együttes térfogatuk az eredeti gúla térfogatának ![]() része. A tetraédert négy egybevágó egyenlőszárú háromszög határolja, ezek alapja
része. A tetraédert négy egybevágó egyenlőszárú háromszög határolja, ezek alapja ![]() , szárai
, szárai ![]() hosszúságúak. A tetraéder egyik csúcsának a szemközti laptól való távolsága megegyezik a metsző síknak a vele párhuzamos gúlalaptól való távolságával.
hosszúságúak. A tetraéder egyik csúcsának a szemközti laptól való távolsága megegyezik a metsző síknak a vele párhuzamos gúlalaptól való távolságával.
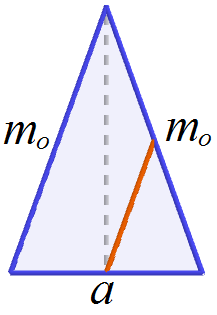
Ezt a távolságot a gúlának az alapnégyzet középvonalára illeszkedő szimmetriasíkjával alkotott metszetéből könnyen meg tudjuk állapítani. A háromszög oldalai ![]() ,
, ![]() ,
, ![]() . A terület kétféle kiszámításából az
. A terület kétféle kiszámításából az ![]() oldalhoz tartozó magasság
oldalhoz tartozó magasság ![]() .
.
A keresett távolság az ![]() oldalhoz tartozó magasság fele,
oldalhoz tartozó magasság fele, ![]() . A tetraéder térfogata pedig
. A tetraéder térfogata pedig 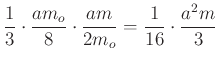 , a gúla térfogatának
, a gúla térfogatának ![]() része. A metsző sík az eredeti gúlát olyan részekre bontja, amelyek térfogatának aránya
része. A metsző sík az eredeti gúlát olyan részekre bontja, amelyek térfogatának aránya 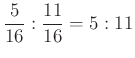 .
.
Leírásunkban csak a teljesség kedvéért szerepeltetjük a számításokat. Tanári bemutató mellett kérdésekkel, ötletadó táblai rajzokkal segíthetünk a számítások elvégzésében.
Ha önálló feldolgozásra szánjuk a GeoGebra munkalapot, akkor bővíthetjük a számítási ötletek megtalálását szolgáló Segítségekkel, és az eredmény ellenőrzésére szolgáló Beviteli mezővel. A Beviteli mező alkalmazására jó példák bőségesen találhatók a GeoGebra adatbázisban. Ilyen például a https://www.geogebra.org/m/eR9S9Epw munkalap, amely egy térgeometriai témához, a csonkakúp térfogatának kiszámításához 2D környezetben készült (Száldobágyi).
A GeoGebra 3D-s nézet használata nélkül is végezhetünk térbeli vizsgálatokat. A 9. ábra egy olyan GeoGebra munkalap képernyőkivágásait mutatja, amelyben Szerkesztés — Kép beszúrása — Fájl parancssorral két részletben (felső és alsó rész) beolvastuk M. C. Escher Belvedere című képét. A felső részt változatlanul, az alsó részt viszont ugyanarra a helyre kétféleképpen olvastuk be — az egyik változat az eredeti állás, a másik a vízszintesen tükrözött változat. Létrehoztunk egy Csúszkát, és úgy állítottuk be a láthatóságot, hogy a Csúszka ![]() értékénél az eredeti, a „lehetetlen” épület, az
értékénél az eredeti, a „lehetetlen” épület, az ![]() érték mellett pedig a trükköt leleplező tükörkép látható.
érték mellett pedig a trükköt leleplező tükörkép látható.

9. ábra: M. C. Escher Belvedere című képének titka (Vásárhelyi 2018a https://ggbm.at/QbuT5Hcs). A kép forrása: https://en.wikipedia.org/wiki/Belvedere(M.C.Escher)
A képhez kapcsolódóan számos probléma vethető fel (centrális vetítés, projektív geometria, stb. Ezekről és más ötletekről olvashatunk Koren és Vásárhelyi elektronikus jegyzetében:
http://ttomc.elte.hu/sites/default/files/kiadvany/tamop-geotanar.pdf.
Irodalomjegyzék
- [1] Hajnal Imre, dr. Nemetz Tibor, dr. Pintér Lajos, dr. Urbán János (1982). Matematika. Fakultatív B változat. Gimnázium IV. osztály, Nemzeti Tankönyvkiadó
- [2] Koren Balázs, Vásárhelyi Éva (2013). Goemetria tanároknak. Elektronikus jegyzet. http://ttomc.elte.hu/sites/default/files/kiadvany/tamop-geotanar.pdf
- [3] Száldobágyi Zsigmond: Csonka-kúp térfogata GeoGebra munkalap. https://www.geogebra.org/m/eR9S9Epw
- [4] Vásárhelyi, É. (2018a). A Belvedere titka — GeoGebra munkalap. https://ggbm.at/QbuT5Hcs
- [5] Vásárhelyi, É. (2018b). A kocka, a kockába írt szabályos tetraéder és a szabályos oktaéder láthatósága Jelölőnégyzettel szabályozva. https://ggbm.at/gr292jkN
- [6] Vásárhelyi, É. (2018c). Kockába írt szabályos tetraéder és oktaéder Csúszkával szabályozva — GeoGebra munkalap. https://ggbm.at/wTfsh8qV
- [7] Vásárhelyi, É. (2018d). Szabályos négyoldalú gúla metszete síkkal — GeoGebra munkalap. https://ggbm.at/J9KmhzeA
- [8] Wertheimer, M. (1912). Experimentelle Studien über das Sehen von Bewegung. (A mozgáslátás kísérleti vizsgálatai) Zeitschrift für Psychologie, 61, 161—265. [Experimental Studies on the Seeing of Motion. English translation in T. Shipley, ed., Classics in Psychology. New York: Philosophical Library, 1961]









