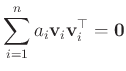Ajánló Jiří Matoušek Thirty-three miniatures. Mathematical and algorithmic applications of linear algebra című könyvéhez
„A lineáris algebra szó hallatán sokakban unalmas és hatalmas mátrixszorzások (rém)képe merül fel, mások pedig valamilyen iszonyúan elvont és emészthetetlen elméletre gondolnak. A könyvben megpróbáljuk ezeket a tévhiteket eloszlatni azáltal, hogy a konkrétból kiindulva haladunk az általános felé, és már minimális tudással felvértezve is valódi és szórakoztató alkalmazásokat tárgyalunk.” (Freud Róbert: Lineáris algebra [2])
A fenti idézet, amely bizonyára sokaknak ismerősen cseng1, akár a jelen ajánló tárgyát képező könyv mottója is lehetne. Jiří Matoušek2 a lineáris algebra számára legkedvesebb, gyakran meglepő alkalmazásait tárja az olvasó elé harminchárom rövid fejezetből (miniatúrából) álló gyűjteményében, amely az Amerikai Matematikai Társaság Student Mathematical Library című könyvsorozatának 53. köteteként jelent meg 2010-ben [7]. A sorozat elsődleges célja, hogy ablakot nyisson a modern matematika aktív kutatási területeire, bemutassa fejlődésüket, a legfontosabb kérdéseket és eredményeket, mindezt ráadásul úgy, hogy a szükséges előismeretek lehetőleg ne haladják meg az egyetemi matematika tananyag alapozó kurzusainak kereteit.
A Thirty-three miniatures ennek a követelménynek minden tekintetben megfelel. A szerző az olvasóról csupán annyit feltételez, hogy rendelkezik lineáris algebrai alapismeretekkel, barátságos viszonyt ápol polinomokkal, valamint ismeri a gráfelmélet és az euklideszi geometria alapfogalmait.
A fejezetek Matoušek szubjektív megítélése szerinti nehézségi sorrendben követik egymást. Valóban, a Fibonacci-sorozatról szóló részek (1. és 2. miniatúrák) akár egy középiskolai szakkörön is – megfelelő előkészülettel – feldolgozhatók, míg a későbbi fejezetek megértésében sokat segíthet, ha az olvasó már rendelkezik bizonyos fokú matematikai érettséggel.
Fontos hangsúlyozni, hogy az egyes miniatúrák önállóan is olvasható kerek egészt alkotnak.3 Mindegyik fejezet egy konkrét probléma pontos ismertetésével és motivációjával, valamint a szükséges definíciók és jelölések bevezetésével kezdődik. Ezt rendszerint az adott fejezet gerincét képező tétel kimondása és bizonyítása követi, végül pedig bibliográfiai megjegyzések és hivatkozások.
Természetesen a gyűjtemény a szerző érdeklődését tükrözi (kombinatorika, geometria és számítógép-tudomány), de ezen belül rendkívül szerteágazó a témaválasztás. A bemutatott alkalmazások által érintett főbb területek a teljesség igénye nélkül (zárójelben a vonatkozó fejezetek sorszámai): algoritmusok (1, 10), extremális halmazrendszerek (3, 4, 8, 17, 33), hibajavító kódok (5), kombinatorikus geometria (6, 7, 9, 15, 18, 20, 30), véletlen algoritmusok (11, 24, 27), lehetetlenségi bizonyítások (12, 13), spektrális gráfelmélet (14, 31), polinommódszer (16, 25), diszkrepanciaelmélet (19, 20), leszámlálási problémák (21, 22, 23, 26) és információelmélet (28, 29).
Mindezek miatt a Thirty-three miniatures kiválóan használható a lineáris algebra, a diszkrét matematika, vagy a gráfelmélet kurzusainak kiegészítő tankönyveként.4 Feldolgozható szemináriumokon, speciálkollégiumokon, de akár önállóan is, és mindazok érdeklődésére számot tart, akik szeretnének bepillantást nyerni a fent említett kutatási területekbe. A további elmélyülést a gazdag irodalomjegyzék segíti. Nagyjából A5-ös méretének köszönhetően a könyv egy kabátzsebben is elfér. Mivel egy miniatúra átlagosan öt (a legrövidebb másfél, a leghosszabb tizenegy) oldal hosszú, ezért már rövidebb utazások során is szórakoztató és érdekfeszítő kihívást kínál.
Ízelítőül íme az eredeti fordításán alapuló 9. miniatúra.
9. miniatúra. Egyenlőszögű egyenesek
Könnyű látni, hogy ![]() -ban legfeljebb három egymást páronként derékszögben metsző egyenes adható meg, de más szögek esetén a helyzet bonyolultabb. Például egy szabályos ikozaéder hat főátója szimmetria-okokból egyenlőszögű családot alkot (1. ábra). A következőkben – lineáris algebra segítségével – megmutatjuk, hogy ez a szám maximális. Legfeljebb hány (origón átmenő) egyenes helyezhető el a háromdimenziós térben úgy, hogy bármely kettő által közbezárt szög ugyanakkora legyen? (Ilyen egyenesek családját egyenlőszögűnek nevezzük.)
-ban legfeljebb három egymást páronként derékszögben metsző egyenes adható meg, de más szögek esetén a helyzet bonyolultabb. Például egy szabályos ikozaéder hat főátója szimmetria-okokból egyenlőszögű családot alkot (1. ábra). A következőkben – lineáris algebra segítségével – megmutatjuk, hogy ez a szám maximális. Legfeljebb hány (origón átmenő) egyenes helyezhető el a háromdimenziós térben úgy, hogy bármely kettő által közbezárt szög ugyanakkora legyen? (Ilyen egyenesek családját egyenlőszögűnek nevezzük.)

Bizonyítás. Tekintsünk ![]() egyenlőszögű egyenest
egyenlőszögű egyenest ![]() -ben, amelyek páronként
-ben, amelyek páronként ![]() fokos szöget zárnak be. Legyen
fokos szöget zárnak be. Legyen ![]() az
az ![]() -edik egyenes 1 hosszúságú irányvektora (
-edik egyenes 1 hosszúságú irányvektora (![]() két lehetséges irányítása közül tetszőlegesen választhatunk). Az egyenlőszögűség feltétele azzal ekvivalens, hogy bármely
két lehetséges irányítása közül tetszőlegesen választhatunk). Az egyenlőszögűség feltétele azzal ekvivalens, hogy bármely ![]() párra
párra
Ha ![]() -re
-re ![]() -es oszlopvektorként tekintünk, akkor egyrészt a skalárszorzat definíciója szerint
-es oszlopvektorként tekintünk, akkor egyrészt a skalárszorzat definíciója szerint ![]() , másrészt
, másrészt ![]() egy
egy ![]() -es mátrix.
-es mátrix.
Megmutatjuk, hogy a ![]() (
( ![]() ) mátrixok lineárisan függetlenek a valós szimmetrikus
) mátrixok lineárisan függetlenek a valós szimmetrikus ![]() -es mátrixok vetorterében, amelynek dimenziója
-es mátrixok vetorterében, amelynek dimenziója ![]() . Következésképp
. Következésképp ![]() , ami épp a bizonyítandó állítás.
, ami épp a bizonyítandó állítás.
Tekintsük tehát az általános
lineáris kombinációt. Az egyenletet jobbról és balról rendre a ![]() és
és ![]() vektorokkal szorozva, a mátrixszorzás asszociativitása alapján
vektorokkal szorozva, a mátrixszorzás asszociativitása alapján
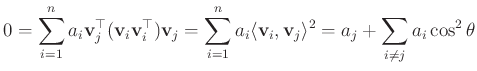
bármely ![]() esetén. Ez az
esetén. Ez az ![]() mátrixegyenlettel ekvivalens, ahol
mátrixegyenlettel ekvivalens, ahol ![]() és
és ![]() . Itt
. Itt ![]() az
az ![]() -es egységmátrixot,
-es egységmátrixot, ![]() pedig a csupa 1-esből álló
pedig a csupa 1-esből álló ![]() -es mátrixot jelöli. Könnyen megmutatható, hogy a
-es mátrixot jelöli. Könnyen megmutatható, hogy a ![]() mátrix nemelfajuló, tehát létezik inverze (ugyanis
mátrix nemelfajuló, tehát létezik inverze (ugyanis ![]() pozitív definit, lásd alább), amiből következik, hogy
pozitív definit, lásd alább), amiből következik, hogy ![]() . De ez pont azt jelenti, hogy az (1) lineáris kombináció triviális, vagyis a
. De ez pont azt jelenti, hogy az (1) lineáris kombináció triviális, vagyis a ![]() (
(![]() ) mátrixok valóban lineárisan függetlenek.
) mátrixok valóban lineárisan függetlenek. ![]()
Feladat. Mutassuk meg, hogy ![]() esetén az
esetén az ![]() mátrix pozitív definit.
mátrix pozitív definit. ![]() az
az ![]() -es egységmátrixot,
-es egységmátrixot, ![]() pedig a csupa 1-esből álló
pedig a csupa 1-esből álló ![]() -es mátrixot jelöli.
-es mátrixot jelöli.
Megjegyzések.
Bár a ![]() felső korlát
felső korlát ![]() esetén éles (amint azt az ikozaéder példája mutatja),
esetén éles (amint azt az ikozaéder példája mutatja), ![]() bizonyos értékeire a becslés tovább élesíthető.
bizonyos értékeire a becslés tovább élesíthető.
Továbbra is nyitott kérdés, hogy általános ![]() esetén legfeljebb mekkora lehet egy egyenlőszögű család,
esetén legfeljebb mekkora lehet egy egyenlőszögű család, ![]() esetén azonban ez a szám pontosan ismert.
esetén azonban ez a szám pontosan ismert. ![]() -re annyit tudunk, hogy egy maximális egyenlőszögű család 28 vagy 29 egyenesből áll. Részletek és további eredmények Greaves, Koolen, Munemasa és Szöllősi 2016-os cikkében találhatók [3].
-re annyit tudunk, hogy egy maximális egyenlőszögű család 28 vagy 29 egyenesből áll. Részletek és további eredmények Greaves, Koolen, Munemasa és Szöllősi 2016-os cikkében találhatók [3].
Legyen most ![]() értéke rögzített, és jelölje
értéke rögzített, és jelölje ![]() egy olyan egyenlőszögű család maximális méretét
egy olyan egyenlőszögű család maximális méretét ![]() -ben, amelyben bármely két egyenes
-ben, amelyben bármely két egyenes ![]() szögben metszi egymást. Balla, Dräxler, Keevash és Sudakov nemrég belátták [1], hogy ekkor
szögben metszi egymást. Balla, Dräxler, Keevash és Sudakov nemrég belátták [1], hogy ekkor ![]() és egyenlőség csakis akkor áll fenn, ha
és egyenlőség csakis akkor áll fenn, ha ![]() . Lásd még a Quanta Magazine kapcsolódó riportját [4].
. Lásd még a Quanta Magazine kapcsolódó riportját [4].
A könyv megrendelhető az AMS honlapjáról: https://bookstore.ams.org/stml-53.
Végül megjegyezzük, hogy a Thirty-three miniatures kiadás előtti változata a hibajegyzékkel együtt elérhető a szerző honlapján: https://kam.mff.cuni.cz/~matousek/la-ams.html.
Irodalomjegyzék
[1] Igor Balla–Felix Dräxler–Peter Keevash–Benny Sudakov: Equiangular lines and spherical codes in Euclidean space, Invent. Math., 211. évf. (2018) 1. sz., 179–212. p. https://doi.org/10.1007/s00222-017-0746-0
-
[2] Róbert Freud: Lineáris algebra. 1996, ELTE Eötvös Kiadó, Budapest, 518. p.
-
[3] Gary Greaves–Jacobus H. Koolen–Akihiro Munemasa–Ferenc Szöllősi: Equiangular lines in Euclidean spaces, J. Combin. Theory Ser. A, 138. évf. (2016), 208–235. p. https://doi.org/10.1016/j.jcta.2015.09.008
-
[4] Kevin Hartnett: A new path to equal-angle lines, https://www.quantamagazine.org/a-new-path-to-equal-angle-lines-20170411. Letöltés dátuma: 2018. február 23.
-
[5] Jan Kratochvíl–Martin Loebl–Jaroslav Nešetřil–Pavel Valtr: Remembering Jiří Matoušek, https://kam.mff.cuni.cz/Matousek-obituary.html. Letöltés dátuma: 2018. február 23.
-
[6] P. W. H. Lemmens–J. J. Seidel: Equiangular lines, J. Algebra, 24. évf. (1973), 494–512. p. https://doi.org/10.1016/0021-8693(73)90123-3.
-
[7] Jiří Matoušek: Thirty-three miniatures. Mathematical and algorithmic applications of linear algebra, Student Mathematical Library sorozat, 53., 2010, American Mathematical Society, Providence, RI, x+182. p. ISBN 978-0-8218-4977-4. https://doi.org/10.1090/stml/053.
-
Huszár Kristóf
- 1 Freud Róbert tankönyve 1996-os megjelenése óta egyetemi hallgatók generációi számara nyújtott bevezetést a lineáris algebrába, amely nemcsak fizikusok és matematikusok és mérnökök mindennapi kenyere, de minden olyan szakterület nélkülözhetetlen eszköztára, ahol felmerül a természetben lejátszódó folyamatok modellezésének, illetve nagymennyiségű (számszerű) adat szisztematikus elemzésének igénye.
- 2 Jiří Matoušek (1963–2015) a prágai Károly Egyetem és a zürichi ETH professzora, generációjának kiemelkedő matematikusa, a kombinatorikus geometria és topológia, illetve a diszkrét matematika nemzetközi hírű kutatója volt. Közel kétszáz tudományos közlemény szerzője vagy társszerzője. Kutatási tevékenysége mellett kivételes tanáregyéniség, nagy hatású pedagógus: az általa írt monográfiák és tankönyvek az adott tudományterületeken alapműnek számítanak [5].
- 3 Kivétel ez alól a 18., illetve a 29. miniatúra, amelyek rendre támaszkodnak a 17., illetve 28. fejezetek eredményeire.
- 4 Jelen sorok írója ezt saját oktatási tapasztalatai alapján is megerősíti.